
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.

【答案】(1)1(2)点P是AB的中点
【解析】
试题分析:(1)由题意得:PD=PE,∠DPE=90°,又由正方形ABCD的边长为1,易证得△ADP≌△QPE,然后由全等三角形的性质,求得线段PQ的长;
(2)易证得△DAP∽△PBF,又由△PFD∽△BFP,根据相似三角形的对应边成比例,可得证得PA=PB,则可求得答案.
试题解析:(1)根据题意得:PD=PE,∠DPE=90°,
∴∠APD+∠QPE=90°,
∵四边形ABCD是正方形,
∴∠A=90°,
∴∠ADP+∠APD=90°,
∴∠ADP=∠QPE,
∵EQ⊥AB,
∴∠A=∠Q=90°,
在△ADP和△QPE中,
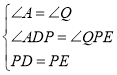 ,
,
∴△ADP≌△QPE(AAS),
∴PQ=AD=1;
(2)∵△PFD∽△BFP,
∴![]() ,
,
∵∠ADP=∠EPB,∠CBP=∠A,
∴△DAP∽△PBF,
∴![]() ,
,
∴![]() ,
,
∴PA=PB,
∴PA=![]() AB=
AB=![]()
∴当PA=![]() ,即点P是AB的中点时,△PFD∽△BFP.
,即点P是AB的中点时,△PFD∽△BFP.



 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】(1)例:代数式(a+b)2表示a、b两数和的平方.仿照上例填空:
代数式a2﹣b2表示_____.
代数式(a+b)(a﹣b)表示_____.
(2)试计算a、b取不同数值时,a2﹣b2及(a+b)(a﹣b)的植,填入下表:

(3)请你再任意给a、b各取一个数值,并计算a2﹣b2及(a+b)(a﹣b)的植:
当a=_____,b=_____时,a2﹣b2=_____,(a+b)(a﹣b)=_____.
(4)我的发现:_____.
(5)用你发现的规律计算:78.352﹣21.652.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,他们共做了60次试验,试验的结果如下:
![]()
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店去买笔,然后走回家,如图是张阳离家的距离与时间的关系图象.
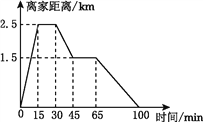
根据图象回答下列问题:
(1)体育场离张阳家多少千米?
(2)体育场离文具店多少千米?张阳在文具店逗留了多长时间?
(3)张阳从文具店到家的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,M![]() 表示a,b,c这三个数的平均数,min
表示a,b,c这三个数的平均数,min![]() 表示a,b,c这三个数中最小的数,如:
表示a,b,c这三个数中最小的数,如:
M![]() ,min
,min![]() =-1;
=-1;
M![]() ,min
,min![]() =
=![]() ;
;
解决下列问题:
(1) 填空:min{ a, a-1, a+2 }=______________;
(2) 若min![]() =2,则x的取值范围是______________;
=2,则x的取值范围是______________;
(3) ①若M![]() =min
=min![]() ,那么x=______________;
,那么x=______________;
②根据①,你发现结论“若M![]() =min
=min![]() ,则______________;(填a,b,c的大小关系);
,则______________;(填a,b,c的大小关系);
③运用②解决问题:(写出求解的过程)
若M![]() =min
=min![]() ,
,
求x+y 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬季即将来临,是流感的高发期,某中学积极进行班级环境消毒,总务处购买甲、乙两种消毒液共100瓶,购买这两种消毒液共用780元,其中甲种消毒液共用240元,且乙种消毒液的单价是甲种消毒液单价的1.5倍.
(1)求甲、乙两种消毒液的单价各为多少元?
(2)该校准备再次购买这两种消毒液(不包括已购买的100瓶),共140瓶,且所需费用不超过1210元,问甲种消毒液至少要购买多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在图 (每个小正方形的边长均为1)中建立两个不同的平面直角坐标系,在各个坐标系中分别写出六边形6个顶点的坐标;
(2)要使图中点B与点F的横坐标互为相反数,则应选取怎样的直线作为y轴,试在图中标出来,此时点E与点C的横坐标有什么关系?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com