
����Ŀ������������a��b��c��M![]() ��ʾa��b��c����������ƽ������min
��ʾa��b��c����������ƽ������min![]() ��ʾa��b��c������������С�������磺
��ʾa��b��c������������С�������磺
M![]() ��min
��min![]() ����1��
����1��
M![]() ��min
��min![]() ��
��![]() ��
��
����������⣺
(1) ��գ�min�� a, a-1, a+2 ����______________��
(2) ��min![]() ��2����x��ȡֵ��Χ��______________��
��2����x��ȡֵ��Χ��______________��
(3) ����M![]() ��min
��min![]() ����ôx��______________��
����ôx��______________��
�ڸ��ݢ٣��㷢�ֽ�������M![]() ��min
��min![]() ����______________������a��b��c�Ĵ�С��ϵ����
����______________������a��b��c�Ĵ�С��ϵ����
�����âڽ�����⣺(д�����Ĺ���)
��M![]() ��min
��min![]() ��
��
��x��y ��ֵ.
���𰸡� a-1 0��x��1 ��1 ��a��b��c��x+y=-4��
�������������������1���ȱȽ�a, a-1, a+2�Ĵ�С���ٸ���������ɵó��𰸣�
��2���ȸ�����������г�����ʽ�飬�ٽ�����⼴�ɵó��𰸣�
��3���������й涨��M{a��b��c}��ʾ����������ƽ������min{a��b��c}��ʾa��b��c���������е���С�����г������鼴����⣮
�⣺��1����a-1<a<a+2��
��min�� a, a-1, a+2 ����a-1��
��2��������ã�
![]() ��
��
��ã�0��x��1��
��3����M{2��x+1��2x}=![]() =x+1=min{2��x+1��2x}��
=x+1=min{2��x+1��2x}��
��![]() ��
��
��![]() ��
��
��x=1��
����M{a��b��c}=min{a��b��c}����a=b=c��
�۸��ݢڵã�2x+y+2=x+2y=2x-y��
��ã�x=-3��y=-1��
��x+y=-4��


 ��ĩ100�ִ��غ�������ϵ�д�
��ĩ100�ִ��غ�������ϵ�д� Сѧ�������Ծ�ϵ�д�
Сѧ�������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ��һ����ϼ����壬�ұ�������������ͼ�����ұߺ�������д��������ͼ�����ƣ�

������������������������ ��ͼ������������ ��ͼ
(2)����������ͼ�гߴ�(��λ��cm)�����������ϼ�����ı������(��ȡ3.14)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̴�λ�������㷨ͳ�ڡ���һ���й���ͳ��ѧ��Ҫ���������ڡ��㷨ͳ�ڡ��м��أ���ƽ����ǧδ��̤�����һ�ߣ����ж��������룬����˸����ǣ���Ů�����������ճ�Ц�ﻶ�ң�������ʿ�غ��棬��������м�������ע�͡�1��=5�ߣ�
���ģ�������ǧ��ֹʱ����ǧ�ϵ�̤�������1�߸ߣ��罫��ǧ��̤����ǰ�ƶ�������10�ߣ�ʱ��̤��ͺ���һ���ߣ���֪�����������5�ߣ������Ĺ���Ͳ����ǣ�ÿ�춼��������ǧ������Ц�����ղ��ϣ�������ܹ��ɽ������������ǧ���������Ƕ�������
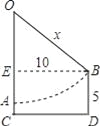
��ͼ��������ǧ��������ʼ�ձ���ֱ��״̬��OA����ǧ�ľ�ֹ״̬��A��̤�壬CD�ǵ��棬��B���ƶ�������̤���λ�ã���AB��̤���ƶ��Ĺ켣����֪AC=1�ߣ�CD=EB=10�ߣ��˵�����BD=5�ߣ���������OA=OB=x�ߣ�����з���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���ڡ�ABC�У���B����C��ADƽ�֡�BAC��E���߶�AD(��ȥ�˵�A��D)��һ���㣬EF��BC�ڵ�F.
(1)����B��40�㣬��DEF��10�㣬���C�Ķ�����
(2)��E��AD���ƶ�ʱ����B����C����DEF֮����������ĵ�����ϵ����д�����������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y1����![]() x�뷴��������y2��
x�뷴��������y2��![]() ��ͼ��A����2��1���㣬��
��ͼ��A����2��1���㣬��
��1�������������Ľ���ʽ��
��2���������뷴����������һ������B�����꣮
��3����x��ʲô��Χ��y1��y2����x��ʲô��Χ��y1��y2����x��ʲô��Χ��y1��y2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1��AB������һ����P������PD���߶�PD�Ƶ�P˳ʱ����ת90��õ��߶�PE����PE��BC��F������DF������E��EQ��AB���ӳ����ڵ�Q��
��1�����߶�PQ�ij���
��2���ʣ���P�ںδ�ʱ����PFD�ס�BFP����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ����̽����
��![]() ����ͼ�۲���֪
����ͼ�۲���֪![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ������Ϊ
������Ϊ![]() ������ͼ�зֱ����
������ͼ�зֱ����![]() ��
��![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ��
��![]() ��λ�ã���д�����ǵ����꣺
��λ�ã���д�����ǵ����꣺![]() __________��
__________��![]() __________��
__________��
�����뷢�֣�
��![]() �����ͼ�ι۲��������������꣬��ᷢ�֣�����ƽ������һ��
�����ͼ�ι۲��������������꣬��ᷢ�֣�����ƽ������һ��![]() ���ڵ�һ�������Ľ�ƽ����
���ڵ�һ�������Ľ�ƽ����![]() �ĶԳƵ�
�ĶԳƵ�![]() ������Ϊ__________������֤������
������Ϊ__________������֤������
�������ع㣺
��![]() ����֪����
����֪����![]() ��
��![]() ������ֱ��
������ֱ��![]() ��ȷ��һ��
��ȷ��һ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() ����ľ���֮����С�������
����ľ���֮����С�������![]() �����꣮
�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
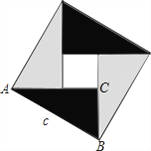
����Ŀ���й��Ŵ���ѧ���Ƕ��ڹ��ɶ����ķ��ֺ�֤������������ѧʷ�Ͼ��ж��صĹ��͵�λ����������ѧ�о��еļ̳кͷ�չ.����4��ȫ�ȵ�ֱ��������ƴ����ͼ��ʾ����ͼ��.Rt��ABC�У���ACB=90�㣬��![]() �������������ͼ�ν���������⣺
�������������ͼ�ν���������⣺
��1����˵��![]() ��
��
��2������������ε������10��С�����ε������2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ܻ���x��1����x99+x98+��+��+x+1�������������ĸ�������ʱ�����ǿ����ȴӼ��������֣�Ȼ����ɳ�һЩ������
��1���ֱ����и�ʽ��
��x��1����x+1��=��������������
��x��1����x2+x+1��=��������������
��x��1����x3+x2+x+1��=��������������
��
��x��1����x99+x98+��+x+1��=��������������
��2��������������Ľ��ۼ��㣺
299+298+��+2+1
399+398+��+3+1
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com