
����Ŀ���̴�λ�������㷨ͳ�ڡ���һ���й���ͳ��ѧ��Ҫ���������ڡ��㷨ͳ�ڡ��м��أ���ƽ����ǧδ��̤�����һ�ߣ����ж��������룬����˸����ǣ���Ů�����������ճ�Ц�ﻶ�ң�������ʿ�غ��棬��������м�������ע�͡�1��=5�ߣ�
���ģ�������ǧ��ֹʱ����ǧ�ϵ�̤�������1�߸ߣ��罫��ǧ��̤����ǰ�ƶ�������10�ߣ�ʱ��̤��ͺ���һ���ߣ���֪�����������5�ߣ������Ĺ���Ͳ����ǣ�ÿ�춼��������ǧ������Ц�����ղ��ϣ�������ܹ��ɽ������������ǧ���������Ƕ�������
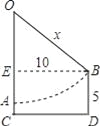
��ͼ��������ǧ��������ʼ�ձ���ֱ��״̬��OA����ǧ�ľ�ֹ״̬��A��̤�壬CD�ǵ��棬��B���ƶ�������̤���λ�ã���AB��̤���ƶ��Ĺ켣����֪AC=1�ߣ�CD=EB=10�ߣ��˵�����BD=5�ߣ���������OA=OB=x�ߣ�����з���Ϊ ��
 ������ϵ�д�
������ϵ�д� �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C��������С����λ�ó������Σ��־���������С��֮����һ�����ﳬ�У�ʹ���е�����С���ľ�����ȣ�����Ӧ����( )

A. ��AC��BC���߸��ߵĽ��㴦
B. ��AC��BC�������ߵĽ��㴦
C. ��AC��BC���ߴ�ֱƽ���ߵĽ��㴦
D. ����A����B���ڽ�ƽ���ߵĽ��㴦
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У���B����C��ƽ�����ཻ�ڵ�O����BO��CO�Ĵ�ֱƽ���߷ֱ�BC�ڵ�E��F.С��˵����E��F��BC�����ȷֵ㣮����ͬ������˵������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1) ![]() ��
��![]() ��(��2)��3��
��(��2)��3��
(2)(��3ab)��(��a2c)3��5b2(c2)3��
(3)x2(x��1)��x(x2��x��1)��
(4)(a��3)(a��1)��a(a��2)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�������20 km���ס������˶���A��ȥB������ͼ��l1��l2�ֱ��ʾ�ס�����������·��s(km)��ʱ��t(h)֮��Ĺ�ϵ������˵��������������1 h�����ҳ���3 h���ϼף��ۼ��ٶ���4 km/h�������ȵ���B����������ȷ�ĸ�����(����)

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Сӱ��С����λͬѧ��ѧϰ��������ʱ����Ͷ�����ӣ��ʵؾ��ȵ������壩���飬���ǹ�����60�����飬����Ľ�����£�
![]()
��1��������3�㳯������Ƶ�ʺ���5�㳯������Ƶ��.
��2��Сӱ˵���������������飬һ�������г���5�㳯�ϵĸ����������С��˵�������Ͷ��600�Σ���ô����6�㳯�ϵĴ���������100����.Сӱ��С���˵����ȷ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����Ϊ8�ľ���ABOC�ı�OB��OC�ֱ���x�ᡢy����������ϣ���A��˫����y��![]() ��ͼ���ϣ���AC��2��
��ͼ���ϣ���AC��2��
��1����kֵ��
��2������BDEF��BD��x����������ϣ�F��AB�ϣ���BD��OC��BF��OB��˫���߽�DE��M�㣬��EF��N�㣬����MEN�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������a��b��c��M![]() ��ʾa��b��c����������ƽ������min
��ʾa��b��c����������ƽ������min![]() ��ʾa��b��c������������С�������磺
��ʾa��b��c������������С�������磺
M![]() ��min
��min![]() ����1��
����1��
M![]() ��min
��min![]() ��
��![]() ��
��
����������⣺
(1) ��գ�min�� a, a-1, a+2 ����______________��
(2) ��min![]() ��2����x��ȡֵ��Χ��______________��
��2����x��ȡֵ��Χ��______________��
(3) ����M![]() ��min
��min![]() ����ôx��______________��
����ôx��______________��
�ڸ��ݢ٣��㷢�ֽ�������M![]() ��min
��min![]() ����______________������a��b��c�Ĵ�С��ϵ����
����______________������a��b��c�Ĵ�С��ϵ����
�����âڽ�����⣺(д�����Ĺ���)
��M![]() ��min
��min![]() ��
��
��x��y ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ĸ���������BC=B��C����AC=A��C������A��CA=��B��CB����AB=A��B���У���ȡ����Ϊ���������µ�һ��Ϊ���ۣ��������Թ�����ȷ�Ľ��۵ĸ����ǣ� ��

A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com