练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：

    (1) －＋(－2)－3；

    (2)(－3ab)·(－a2c)3·5b2(c2)3；

    (3)x2(x－1)－x(x2＋x－1)；

    (4)(a＋3)(a－1)＋a(a－2)．

    【答案】(1)- (2) 15a7b3c9 (3)－2x2＋x (4) 2a2－3

    【解析】试题分析：（1）根据乘方的定义、零指数幂的性质、负整数指数幂的性质分别计算各项后合并即可；（2）先算乘方，再算乘除即可；（3）根据单项式乘以多项式的运算法则计算后，再合并同类项即可；（4）根据多项式乘以多项式的运算法则和单项式乘以多项式的运算法则计算后，再合并同类项即可.

    试题解析：

    (1)原式＝－－1－＝－.

    (2)原式＝－3ab·(－a6c3)·5b2·c6＝15a7b3c9.

    (3)原式＝x3－x2－x3－x2＋x＝－2x2＋x.

    (4)原式＝a2＋2a－3＋a2－2a＝2a2－3.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

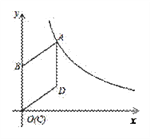
    【题目】如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数（k＞0，x＞0）的图象上，点D的坐标为（，2）．

    （1）求k的值；

    （2）若将菱形ABCD沿x轴正方向平移，当菱形的一个顶点恰好落在函数（k＞0，x＞0）的图象上时，求菱形ABCD平移的距离；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)如图是一个组合几何体，右边是它的两种视图，在右边横线上填写出两种视图的名称；

    　　　　　　　　　　　　 视图　　　　　　 视图

    (2)根据两种视图中尺寸(单位：cm)，计算这个组合几何体的表面积．(π取3.14)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB =AC=2，∠B = 40°，点D在线段BC上运动（不与点B，C重合），连接AD，作∠ADE = 40°，DE交线段AC于点E．

    （1）当∠BDA = 115°时，∠BAD= °，∠DEC = °，当点D从点B向点C运动时，∠BDA逐渐变 （填“大”或“小”） ．

    （2）当DC等于多少时，△ABD≌△DCE？请说明理由．

    （3）在点D的运动过程中，是否存在△ADE是等腰三角形？若存在，请直接写出此时∠BDA的度数；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线分别与轴、轴交于点、，且与直线交于点．

    （1）若是线段上的点，且的面积为，求直线的函数表达式．

    （）在（）的条件下，设是射线上的点，在平面内是否存在点，使以、、、为顶点的四边形是菱形？若存在，直接写出点的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为1个单位长度的小正方形组成的网格中．

    （1）把 平移至的位置，使点与对应，得到；

    （2）运用网格画出边上的高所在的直线，标出垂足；

    （3）线段与的关系是_____________；

    （4）如果是按照先向上4格，再向右5格的方式平移到，那么线段在运动过程中扫过的面积是___________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】程大位所著《算法统宗》是一部中国传统数学重要的著作．在《算法统宗》中记载：“平地秋千未起，踏板离地一尺．送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几？”【注释】1步=5尺．

    译文：“当秋千静止时，秋千上的踏板离地有1尺高，如将秋千的踏板往前推动两步（10尺）时，踏板就和人一样高，已知这个人身高是5尺．美丽的姑娘和才子们，每天都来争荡秋千，欢声笑语终日不断．好奇的能工巧匠，能算出这秋千的绳索长是多少吗？”

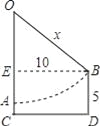
    如图，假设秋千的绳索长始终保持直线状态，OA是秋千的静止状态，A是踏板，CD是地面，点B是推动两步后踏板的位置，弧AB是踏板移动的轨迹．已知AC=1尺，CD=EB=10尺，人的身高BD=5尺．设绳索长OA=OB=x尺，则可列方程为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，在△ABC中，∠B＜∠C，AD平分∠BAC，E的线段AD(除去端点A、D)上一动点，EF⊥BC于点F.

    (1)若∠B＝40°，∠DEF＝10°，求∠C的度数．

    (2)当E在AD上移动时，∠B、∠C、∠DEF之间存在怎样的等量关系？请写出这个等量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

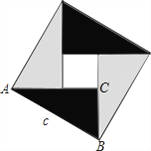
    【题目】中国古代数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位，体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中，∠ACB=90°，若，请你利用这个图形解决下列问题：

    （1）试说明；

    （2）如果大正方形的面积是10，小正方形的面积是2，求的值．

    查看答案和解析>>

    同步练习册答案