Question

【题目】如图，在平面直角坐标系中，直线分别与轴、轴交于点、，且与直线交于点．

（1）若是线段上的点，且的面积为，求直线的函数表达式．

（）在（）的条件下，设是射线上的点，在平面内是否存在点，使以、、、为顶点的四边形是菱形？若存在，直接写出点的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）（2）存在，或或

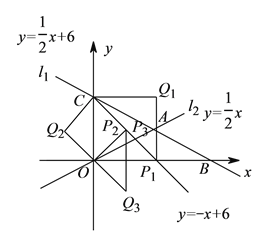
【解析】试题分析：(1)对于直线解析式,令x=0，求出y的值,确定C的坐标；根据D在直线OA上,设,表示出△COD面积,把已知面积代入求出x的值,确定出D坐标,利用待定系数法求出CD解析式即可；

(2)在(1)的条件下,设P是射线CD上的点,在平面内存在点Q,使以O、C、P、Q为顶点的四边形是菱形,如图所示,分三种情况考虑:①当四边形为菱形时,由,得到四边形为正方形;②当四边形为菱形时;③当四边形为菱形时;分别求出Q坐标即可.

解：（）设．

∵且，

∴

∴

∴．

令直线解析式为

把，代入得：

∴．

∴．

（）存在．

①当四边形为菱形时．

∵得四边形为正方形

∴,

即．

②当四边形为菱形时

∵得

代入得，

∴．

③当四边形为菱形时

∴

∴

综上得点的坐标为或或．