
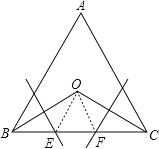
【题目】如图,在等边三角形ABC中,∠B、∠C的平分线相交于点O,作BO、CO的垂直平分线分别交BC于点E、F.小明说:“E、F是BC的三等分点.”你同意他的说法吗?请说明理由.

【答案】同意,理由见解析
【解析】试题分析:连接OE、OF,根据等边三角形角平分线的性质,可得∠OBC=∠OCB=30°,由BC的垂直平分线,可知BE=OE,∠EBO=∠EOB=30°,∠OEF=60°,再证,∠OFE=60°,得出△OEF为等边三角形,从而可知EF=OE=BE=OF=FC,得出结论.
试题解析:同意.理由如下:
连接OE、OF,
∵E为BO垂直平分线上的点,且∠OBC=30°,
∴BE=OE,∠EBO=∠EOB=30°,
∴∠OEF=∠EBO+∠EOB=60°,
同理,∠OFE=∠FCO+∠FOC=60°,
∴△OEF为等边三角形,
即EF=OE=BE,EF=OF=FC,
故E、F为BC的三等分点,
故该说法正确.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
⑴画出△ABC向右平移4个单位后得到的△A1B1C1;
⑵图中AC与A1C1的关系是: ;
⑶画出△ABC中AB边上的中线CD;
⑷△ACD的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:整式乘法与因式分解是方向相反的变形
由(x+p)(x+q)=x2+(p+q)x+pq得x2+(p+q)x+pq=(x+p)(x+q)
利用这个式子可以将某些二次项系数是1的二次三项式分解因式,
例如:将式子x2+3x+2分解因式.
分析:这个式子的常数项2=1×2一次项系数3=1+2
所以x2+3x+2=x2+(1+2)x=1×2
解:x2+3x+2=(x+)(x+2)
请仿照上面的方法,解答下列问题:
(1)分解因式:x2+6x-27=__________________;
(2)若x2+px+8可分解为两个一次因式的积,则整数![]() 的所有可能值是_________________;
的所有可能值是_________________;
(3)利用因式分解法解方程:x2-4x-12=0..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图的名称;

视图 视图
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB =AC=2,∠B = 40°,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE = 40°,DE交线段AC于点E.
(1)当∠BDA = 115°时,∠BAD= °,∠DEC = °,当点D从点B向点C运动时,∠BDA逐渐变 (填“大”或“小”) .
(2)当DC等于多少时,△ABD≌△DCE?请说明理由.
(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,且与直线
,且与直线![]() 交于点
交于点![]() .
.

(1)若![]() 是线段
是线段![]() 上的点,且
上的点,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的函数表达式.
的函数表达式.
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() 是射线
是射线![]() 上的点,在平面内是否存在点
上的点,在平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”【注释】1步=5尺.
译文:“当秋千静止时,秋千上的踏板离地有1尺高,如将秋千的踏板往前推动两步(10尺)时,踏板就和人一样高,已知这个人身高是5尺.美丽的姑娘和才子们,每天都来争荡秋千,欢声笑语终日不断.好奇的能工巧匠,能算出这秋千的绳索长是多少吗?”
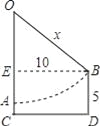
如图,假设秋千的绳索长始终保持直线状态,OA是秋千的静止状态,A是踏板,CD是地面,点B是推动两步后踏板的位置,弧AB是踏板移动的轨迹.已知AC=1尺,CD=EB=10尺,人的身高BD=5尺.设绳索长OA=OB=x尺,则可列方程为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验与探究:
(![]() )由图观察易知
)由图观察易知![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]() ,请在图中分别标明
,请在图中分别标明![]() 、
、![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 、
、![]() 的位置,并写出他们的坐标:
的位置,并写出他们的坐标:![]() __________、
__________、![]() __________.
__________.
归纳与发现:
(![]() )结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点
)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点![]() 关于第一、三象限的角平分线
关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为__________(不必证明).
的坐标为__________(不必证明).
运用与拓广:
(![]() )已知两点
)已知两点![]() 、
、![]() ,试在直线
,试在直线![]() 上确定一点
上确定一点![]() ,使点
,使点![]() 到
到![]() 、
、![]() 两点的距离之和最小,并求出
两点的距离之和最小,并求出![]() 点坐标.
点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com