
【题目】如图是9×7的正方形点阵,其水平方向和竖起直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:

(1)请在图中画出以AB为边且面积为2的一个网格三角形;
(2)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形的面积为2的概率;
(3)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形为直角三角形的概率.
【答案】(1)图形略,共12个三角形;(2)![]() ;(3)
;(3)![]() .
.
【解析】本题考查的是概率公式
可以直接画出一个满足条件的三角形;
(2)首先找出可以组成的所有三角形的个数,然后再计算面积为2的三角形的个数,由此可得到所求的概率;
(3)首先找出可以组成的所有三角形的个数,然后再看其中的直角三角形的个数,由此可得到所求的概率.
(1)如图所示(共12个,这是其中一个):
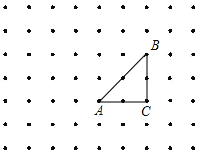
(2)由分析可知:只要M不再AB上或者AB的延长线上,ABM都可以构成三角形,共有9×7-7=63-7=56个,

又∵由(1)知,以A、B、M为顶点的三角形的面积为2的三角形共有12个,
∴以A、B、M为顶点的三角形的面积为2的概率为![]() ;
;
(3)由分析可知:以A、B、M为顶点的直角三角形共有12个,
以A、B、M为顶点的三角形为直角三角形的概率为![]() .
.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】将下列方格纸中的△ABC向右平移7格,再向下平移2格,得到△![]() .(1)画出平移后的三角形;
.(1)画出平移后的三角形;
(2)若AB=5,则![]() = .
= .
(3)连接AA1,BB1, 根据“图形平移”的性质,得:线段AA1与线段BB1的数量关系和位置关系是: .
(4)求图中∠![]() AC+∠
AC+∠![]() BC的度数.
BC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个港口相距72千米,一艘轮船从甲港出发,顺流航行3小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到甲港,并立即返回(掉头时间忽略不计)。已知水流速度是2千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系式,结合图象解答下列问题:
(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度)

(1)轮船在静水中的速度是 千米/时;快艇在静水中的速度是 千米/时;
(2)求快艇返回时的解析式,写出自变量取值范围;
(3)快艇出发多长时间,轮船和快艇在返回途中相距12千米?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, ![]() 是边长为
是边长为![]() 的等边三角形,直线
的等边三角形,直线![]() 与
与![]() 轴、
轴、![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() 、
、![]() .
. ![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(![]() )点
)点![]() 的坐标为__________.(结果保留根号)
的坐标为__________.(结果保留根号)
(![]() )求证:点
)求证:点![]() 、
、![]() 关于
关于![]() 轴对称.
轴对称.
(![]() )若
)若![]() ,求直线
,求直线![]() 对应的函数表达式.
对应的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列证明过程填空:
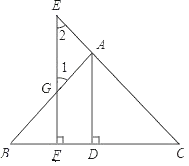
已知:如 图,AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2.
求证:AD平分∠BAC,填写证明中的空白.
证明:
∵AD⊥BC,EF⊥BC (已知),
∴EF∥AD ( ),
∴ = ( 两直线平行,内错角相等 ),
=∠CAD ( ).
∵ (已知),
∴ ,即AD平分∠BAC ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从3,0,-1,-2,-3这五个数中,随机抽取一个数,作为函数y=(5-m2)x和关于x的方程(m+1)x2+mx+1=0中m的值,恰好使所得函数的图象经过第一、三象限,且方程有实数根的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
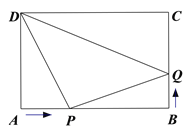
【题目】如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点终点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动,它们到达终点后停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ的面积是24cm2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com