
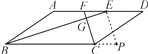
【题目】如图,在ABCD中,∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,BE与CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=3,BC=5,CF=2,求BE的长.
【答案】(1)证明见解析;(2) BE=4![]() .
.
【解析】试题分析:(1)根据平行四边形两组对边分别平行可得∠ABC+∠BCD=180°,再根据角平分线的性质可得∠EBC+∠FCB=![]() ∠ABC+
∠ABC+![]() ∠DCB=90°,进而可得BE⊥CF;
∠DCB=90°,进而可得BE⊥CF;
(2)过A作AM∥FC,首先证明△ABE是等腰三角形,进而得到BO=EO,再利用勾股定理计算出EO的长,进而可得答案.
试题解析:(1)∵BE平分∠ABC,CF平分∠BCD,
∴∠CBE=![]() ∠ABC,∠BCF=
∠ABC,∠BCF=![]() ∠BCD.
∠BCD.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠CBE+∠BCF=![]() (∠ABC+∠BCD)=90°,
(∠ABC+∠BCD)=90°,
∴∠CGB=90°,
∴BE⊥CF.
(2)过点E作EP∥FC,交BC的延长线于点P,
则易证四边形CPEF是平行四边形,所以EP=CF=2,
.∵BE平分∠ABC,
∴∠ABE=∠CBE.
在ABCD中,∵AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE=3.
同理可得DF=DC=3,
∴EF=AE+DF-AD=1,
∴CP=EF=1.
又由(1)已证得BE⊥CF,
∴BE⊥EP,
∴在Rt△BPE中,BE2+EP2=BP2,即BE2+22=62,
所以BE=4![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两个港口相距72千米,一艘轮船从甲港出发,顺流航行3小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到甲港,并立即返回(掉头时间忽略不计)。已知水流速度是2千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系式,结合图象解答下列问题:
(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度)

(1)轮船在静水中的速度是 千米/时;快艇在静水中的速度是 千米/时;
(2)求快艇返回时的解析式,写出自变量取值范围;
(3)快艇出发多长时间,轮船和快艇在返回途中相距12千米?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从3,0,-1,-2,-3这五个数中,随机抽取一个数,作为函数y=(5-m2)x和关于x的方程(m+1)x2+mx+1=0中m的值,恰好使所得函数的图象经过第一、三象限,且方程有实数根的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应我市“中国梦”“宜宾梦”主题教育活动,某中学在全校学生中开展了以“中国梦我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.小明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
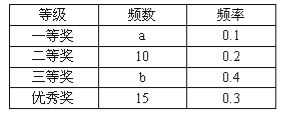
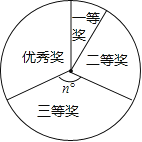
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ,n= .
(2)学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)画出△ABC的AB边上的中线CD;

(2)画出△ABC向右平移4个单位后的△A1B1C1;
(3)图中AC与A1C1的关系是______;
(4)图中△ABC的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
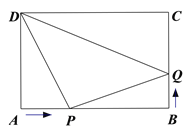
【题目】如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点终点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动,它们到达终点后停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ的面积是24cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
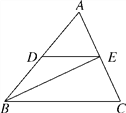
【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com