
����Ŀ����Rt��ABC�У���ACB=90�㣬AB=![]() ��AC=2������B��ֱ��m��AC������ABC�Ƶ�C˳ʱ����ת�õ���A��B��C(��A��B�Ķ�Ӧ��ֱ�ΪA'��B��)������CA�䣬CB��քe��ֱ��m�ڵ�P��Q��
��AC=2������B��ֱ��m��AC������ABC�Ƶ�C˳ʱ����ת�õ���A��B��C(��A��B�Ķ�Ӧ��ֱ�ΪA'��B��)������CA�䣬CB��քe��ֱ��m�ڵ�P��Q��
(1)��ͼ1����P��A���غ�ʱ�����ACA��Ķ�����
(2)��ͼ2����A��B����BC�Ľ���ΪM����MΪA��B����е�ʱ�����߶�PQ�ij���
(3)����ת�����У�����P��Q�ֱ���CA�䣬CB����ӳ�����ʱ����̽���ı���PA'B��Q������Ƿ������Сֵ�������ڣ�����ı���PA��B��Q����С������������ڣ���˵�����ɣ�
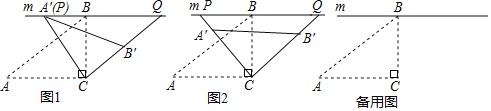
���𰸡���1��60������2��PQ��![]() ����3�����ڣ�S�ı���PA'B��Q��3��
����3�����ڣ�S�ı���PA'B��Q��3��![]()
��������
��1������ת�ɵã�AC=A'C=2�������õ�BC![]() �����ݡ�A'BC=90�����ɵ�cos��A'CB
�����ݡ�A'BC=90�����ɵ�cos��A'CB![]() �����ɵõ���A'CB=30������ACA'=60����
�����ɵõ���A'CB=30������ACA'=60����
��2������MΪA'B'���е㣬���ɵó���A=��A'CM�������õ�PB![]() BC
BC![]() ������tan��Q=tan��A
������tan��Q=tan��A![]() �����ɵõ�BQ=BC
�����ɵõ�BQ=BC![]() 2�������ó�PQ=PB+BQ
2�������ó�PQ=PB+BQ![]() ��
��
��3������S�ı���PA'B'Q=S��PCQ��S��A'CB'=S��PCQ![]() �����ɵõ�S�ı���PA'B'Q��С����S��PCQ��С����S��PCQ
�����ɵõ�S�ı���PA'B'Q��С����S��PCQ��С����S��PCQ![]() PQ��BC
PQ��BC![]() PQ�����ü��η����ɵõ�S��PCQ����Сֵ=3�����ɵõ����ۣ�
PQ�����ü��η����ɵõ�S��PCQ����Сֵ=3�����ɵõ����ۣ�
��1������ת�ɵã�AC=A'C=2��
�ߡ�ACB=90����AB![]() ��AC=2����BC
��AC=2����BC![]() ��
��
�ߡ�ACB=90����m��AC�����A'BC=90������cos��A'CB![]() �����A'CB=30�������ACA'=60����
�����A'CB=30�������ACA'=60����
��2����MΪA'B'���е㣬���A'CM=��MA'C������ת�ɵã���MA'C=��A�����A=��A'CM����tan��PCB=tan��A![]() ����PB
����PB![]() BC
BC![]() ��
��
�ߡ�BQC=��BCP=��A����tan��BQC=tan��A![]() ����BQ=BC
����BQ=BC![]() 2����PQ=PB+BQ
2����PQ=PB+BQ![]() ��
��
��3����S�ı���PA'B'Q=S��PCQ��S��A'CB'=S��PCQ![]() ����S�ı���PA'B'Q��С����S��PCQ��С����S��PCQ
����S�ı���PA'B'Q��С����S��PCQ��С����S��PCQ![]() PQ��BC
PQ��BC![]() PQ��
PQ��
ȡPQ���е�G��
�ߡ�PCQ=90������CG![]() PQ����PQ=2CG����CG��Сʱ��PQ��С����CG��PQ����CG��CB�غ�ʱ��CG��С����CGmin
PQ����PQ=2CG����CG��Сʱ��PQ��С����CG��PQ����CG��CB�غ�ʱ��CG��С����CGmin![]() ��PQmin=2
��PQmin=2![]() ����S��PCQ����Сֵ=3��S�ı���PA'B'Q=3
����S��PCQ����Сֵ=3��S�ı���PA'B'Q=3![]() ��
��



 ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д� ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���A=90����AB=AC��BC=20��DE����ABC����λ�ߣ���M�DZ�BC��һ�㣬BM=3����N���߶�MC�ϵ�һ�����㣬����DN��ME��DN��ME�ཻ�ڵ�O������OMN��ֱ�������Σ���DO�ij���______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶Ϊ5cm����AB��CD��AB��8cm��CD��6cm����AB��CD�ľ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
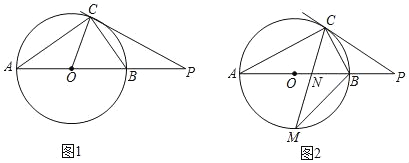
����Ŀ����֪��AB�ǡ�O��ֱ������C�ڡ�O�ϣ���P��AB�ӳ�����һ�㣬����CP��
(1)��ͼ1������PCB����A��
����֤��ֱ��PC�ǡ�O�����ߣ�
����CP��CA��OA��2����CP�ij���
(2)��ͼ2������M�ǻ�AB���е㣬CM��AB�ڵ�N��MNMC��9����BM��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��b��c�dz�����a��0��ͼ���һ���֣���x��Ľ���A�ڵ㣨2��0���ͣ�3��0��֮�䣬�Գ�����x=1����������˵������ab��0����2a+b=0����3a+c��0����a+b��m��am+b����mΪʵ������������1��x��3ʱ��y��0��������ȷ���ǣ�������

A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
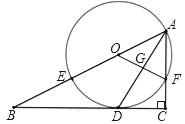
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬ADƽ����BAC��BC�ڵ�D��OΪAB��һ�㣬������A��D����O�ֱ�AB��AC�ڵ�E��F������OF��AD�ڵ�G��
(1)��֤��BC����O�����ߣ�
(2)��AB=x��AF=y�����ú�x��y�Ĵ���ʽ��ʾ�߶�AD�ij���
(3)��BE=8��sinB=![]() ����DG�ij���
����DG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��һ������վ��ڵ�˫��բ������ͼ2������˫��չ��ʱ��˫����Ե�Ķ˵�A��B֮��ľ���Ϊ10cm��˫���ı�ԵAC��BD��54cm������բ��������нǡ�PCA����BDQ��30�㣮��˫������ʱ������ͨ��բ���������������Ϊ(����)

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC�����Բ����O��BC���ϣ���BAC��ƽ���߽���O�ڵ�D������BD��CD������D��BC��ƽ������AC���ӳ����ཻ�ڵ�P��
��1����֤��PD����O�����ߣ�
��2����֤��ABCP��BDCD��
��3����AB��5cm��AC��12cmʱ�����߶�PC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
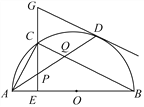
����Ŀ����ͼ���ڡ�O�У�AB��ֱ������D�ǡ�O��һ�㣬��C��![]() ���е㣬CE��AB�ڵ�E������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CE��CB�ڵ�P��Q������AC���������н��ۣ��١�BAD����ABC����GP��GD���۵�P�ǡ�ACQ�����ģ����н�����ȷ����________(ֻ����д���)��
���е㣬CE��AB�ڵ�E������D�����߽�EC���ӳ����ڵ�G������AD���ֱ�CE��CB�ڵ�P��Q������AC���������н��ۣ��١�BAD����ABC����GP��GD���۵�P�ǡ�ACQ�����ģ����н�����ȷ����________(ֻ����д���)��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com