
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(2011山东济南,22,3分)如图1,△ABC中,∠C=90°,∠ABC=30°,AC=m,延长CB至点D,使BD=AB.
①求∠D的度数;
②求tan75°的值.
(2)如图2,点M的坐标为(2,0),直线MN与y轴的正半轴交于点N,∠OMN=75°.求直线MN的函数表达式.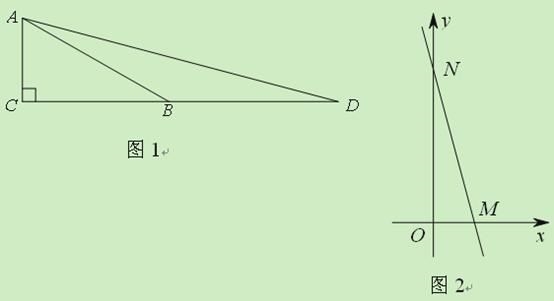
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正三角形和正方形内接于同一个圆;如图②,正方形和正五边形内接于同一个圆;如图③,正五边形和正六边形内接于同一个圆;…;则对于图①来说,BD可以看作是正_____边形的边长;若正n边形和正(n+1)边形内接于同一个圆,连接与公共顶点相邻同侧两个不同正多边形的顶点可以看做是_____边形的边长.
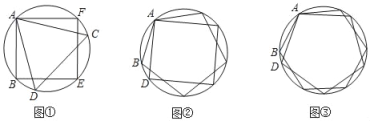
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,图象经过B(﹣3,0)、C(0,3)两点,且与x轴交于点A.
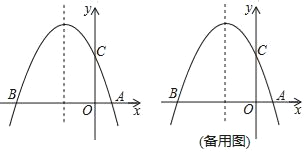
(1)求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)在抛物线的对称轴上找一点M,使△ACM周长最短,求出点M的坐标;
(3)若点P为抛物线对称轴上的一个动点,直接写出使△BPC为直角三角形时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC,∠BAC=90°,BC=5,AC=2![]() ,以A为圆心、AB为半径画圆,与边BC交于另一点D.
,以A为圆心、AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的正弦值.
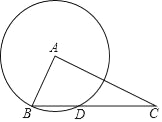
查看答案和解析>>
科目:初中数学 来源: 题型:
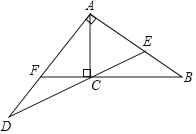
【题目】如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.
(1)求CF的长;
(2)求∠D的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
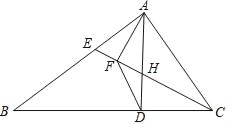
【题目】如图,在△ABC中,点D在边BC上,∠CAD=∠B,点E在边AB上,联结CE交AD于点H,点F在CE上,且满足CFCE=CDBC.
(1)求证:△ACF∽△ECA;
(2)当CE平分∠ACB时,求证:![]() =
=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
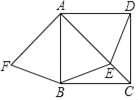
【题目】如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)BF和DE有怎样的数量关系?请证明你的结论;
(2)在其他条件都保持不变的是情况下,当点E运动到AC中点时,四边形AFBE是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
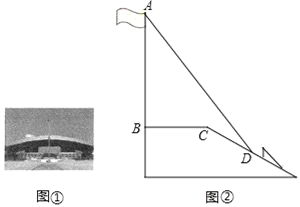
【题目】深圳市民中心广场上有旗杆如图①所示,某学校兴趣小组测量了该旗杆的高度,如图②,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为16米,落在斜坡上的影长CD为8米,AB⊥BC;同一时刻,太阳光线与水平面的夹角为45°.1米的标杆EF竖立在斜坡上的影长FG为2米,求旗杆的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com