
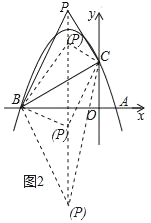
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,图象经过B(﹣3,0)、C(0,3)两点,且与x轴交于点A.
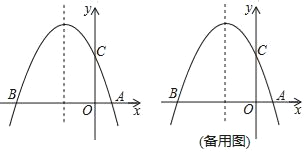
(1)求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)在抛物线的对称轴上找一点M,使△ACM周长最短,求出点M的坐标;
(3)若点P为抛物线对称轴上的一个动点,直接写出使△BPC为直角三角形时点P的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)当点M的坐标为(﹣1,2)时,△ACM周长最短;(3)使△BPC为直角三角形时点P的坐标为(﹣1,﹣2),(﹣1,![]() ),(﹣1,
),(﹣1,![]() )或(﹣1,4).
)或(﹣1,4).
【解析】
(1)由抛物线的对称轴及点B的坐标可求出点A的坐标,由点A,B,C的坐标,利用待定系数法即可求出二次函数的表达式;
(2)连接BC,交直线x=-1于点M,此时△ACM周长最短,由点B,C的坐标,利用待定系数法可求出直线BC的函数表达式,再利用一次函数图象上点的坐标特征即可求出点M的坐标;
(3)设点P的坐标为(-1,m),结合点B,C的坐标可得出PB2,PC2,BC2的值,分∠BCP=90°,∠CBP=90°,∠BPC=90°三种情况考虑,①当∠BCP=90°时,利用勾股定理可得出关于m的一元一次方程,解之可得出m的值,进而可得出点P的坐标;②当∠CBP=90°时,利用勾股定理可得出关于m的一元一次方程,解之可得出m的值,进而可得出点P的坐标;③当∠BPC=90°时,利用勾股定理可得出关于m的一元二次方程,解之可得出m的值,进而可得出点P的坐标.综上,此题得解.
(1)∵二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,点B的坐标为(﹣3,0),
∴点A的坐标为(1,0).
将A(1,0),B(﹣3,0),C(0,3)代入y=ax2+bx+c,
得: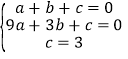 ,
,
解得: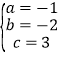 ,
,
∴二次函数的表达式为y=﹣x2﹣2x+3.
(2)连接BC,交直线x=﹣1于点M,如图1所示.
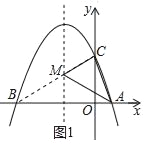
∵点A,B关于直线x=﹣1对称,
∴AM=BM.
∵点B,C,M三点共线,
∴此时AM+CM取最小值,最小值为BC.
设直线BC的函数表达式为y=kx+d(k≠0),
将B(﹣3,0),C(0,3)代入y=kx+d,
得:![]() ,
,
解得:![]() ,
,
∴直线BC的函数表达式为y=x+3.
当x=﹣1时,y=x+3=2,
∴当点M的坐标为(﹣1,2)时,△ACM周长最短.
(3)设点P的坐标为(﹣1,m),
∵点B的坐标为(﹣3,0),点C的坐标为(0,3),
∴PB2=[﹣3﹣(﹣1)]2+(0﹣m)2=m2+4,
PC2=[0﹣(﹣1)]2+(3﹣m)2=m2﹣6m+10,
BC2=[0﹣(﹣3)]2+(3﹣0)2=18.
分三种情况考虑(如图2):
①当∠BCP=90°时,BC2+PC2=PB2,
∴18+m2﹣6m+10=m2+4,
解得:m=4,
∴点P的坐标为(﹣1,4);
②当∠CBP=90°时,BC2+PB2=PC2,
∴18+m2+4=m2﹣6m+10,
解得:m=﹣2,
∴点P的坐标为(﹣1,﹣2);
③当∠BPC=90°时,PB2+PC2=BC2,
∴m2+4+m2﹣6m+10=18,
整理得:m2﹣3m﹣2=0,
解得:m1=![]() ,m2=
,m2=![]() ,
,
∴点P的坐标为(﹣1,![]() )或(﹣1,
)或(﹣1,![]() ).
).
综上所述:使△BPC为直角三角形时点P的坐标为(﹣1,﹣2),(﹣1,![]() ),(﹣1,
),(﹣1,![]() )或(﹣1,4).
)或(﹣1,4).


科目:初中数学 来源: 题型:
【题目】(1)验证下列两组数值的关系:
2sin30°cos30°与sin60°;
2sin22.5°cos22.5°与sin45°.
(2)用一句话概括上面的关系.
(3)试一试:你自己任选一个锐角,用计算器验证上述结论是否成立.
(4)如果结论成立,试用α表示一个锐角,写出这个关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.

(1)请画出这个几何体的三视图;
(2)如图2,如果现在你手头还有一些相同的小正方体,要求保持俯视图和左视图不变,最多可以再添加几个小正方体;
(3)若在这个几何体的表面喷上黄色的漆(靠地面的一面不喷),有________个正方体只有一个面是黄色,有________个正方体三个面是黄色.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D,E,F分别是OA,OB,OC的中点,下面的说法中:①△ABC与△DEF是位似图形;②△ABC与△DEF的相似比为1∶2;③△ABC与△DEF的周长之比为2∶1;④△ABC与△DEF的面积之比为4∶1.正确的是( )
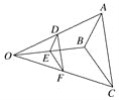
A. ①②③ B. ①③④ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
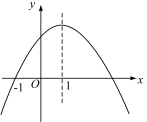
【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(-![]() ,y1),(
,y1),(![]() ,y2)是抛物线上两点,则y1<y2, 其中结论正确的是________.
,y2)是抛物线上两点,则y1<y2, 其中结论正确的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
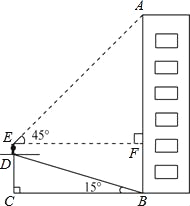
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=
,tan15°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.如图,已知函数y=-2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=-2x+4是“平行一次函数”
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形,位似中心为原点,位似比为1:2,求函数y=kx+b的表达式.
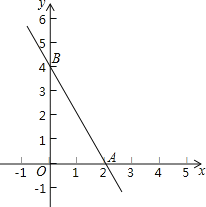
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com