
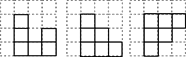
【题目】如图1,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.

(1)请画出这个几何体的三视图;
(2)如图2,如果现在你手头还有一些相同的小正方体,要求保持俯视图和左视图不变,最多可以再添加几个小正方体;
(3)若在这个几何体的表面喷上黄色的漆(靠地面的一面不喷),有________个正方体只有一个面是黄色,有________个正方体三个面是黄色.
【答案】(1)详见解析;(2)最多可再添加4个小正方体;(2)1,3.
【解析】
(1)主视图有三列,每列小正方形数目分别是3,1,2;左视图有三列,每列小正方形数目分别为3,2,1;俯视图有三列,每列小正方形数目分别为3,2,1,据此可画出图形.
(2)保持俯视图和左视图不变,在第二层第二列第二行和第三行各加一个;第三层第二列第三行加一个,第三列第三行加1个,相加可求出.
(3)只有一个面是黄色的是第一列正方体中最底层中间的正方体,只有三个面是黄色的是第一列第二层最后面的正方体,第二列最前面的正方体,第三列最底层的正方体.
解:(1)如图所示:
(2)在第二层第二列第二行和第三行各加一个;第三层第二列第三行加一个,第三列第三行加1个,2+1+1=4(个).故最多可再添加4个小正方体.
(3) 只有一个面是黄色的是第一列正方体中最底层中间的正方体,只有三个面是黄色的是第一列第二层最后面的正方体,第二列最前面的正方体,第三列最底层的正方体,故答案为1,3.


科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,22,3分)如图1,△ABC中,∠C=90°,∠ABC=30°,AC=m,延长CB至点D,使BD=AB.
①求∠D的度数;
②求tan75°的值.
(2)如图2,点M的坐标为(2,0),直线MN与y轴的正半轴交于点N,∠OMN=75°.求直线MN的函数表达式.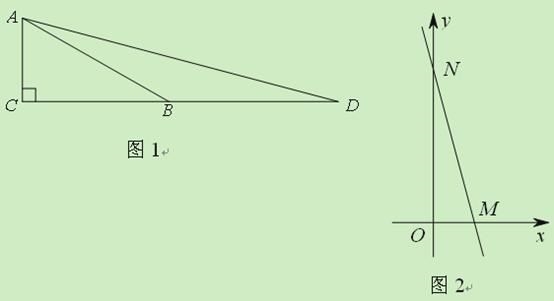
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AO是![]() 的半径,AC为
的半径,AC为![]() 的弦,点F为
的弦,点F为![]() 的中点,OF交AC于点E,AC=8,EF=2.
的中点,OF交AC于点E,AC=8,EF=2.
(1)求AO的长;
(2)过点C作CD⊥AO,交AO延长线于点D,求sin∠ACD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民俗村为了维护消费者利益,限定村内所有商品的利润率不得超过![]() ,村内一商店以每件16元的价格购进一批商品,该商品每件售价定为x元,每天可卖出
,村内一商店以每件16元的价格购进一批商品,该商品每件售价定为x元,每天可卖出![]() 件,每天销售该商品所获得的利润为y元.
件,每天销售该商品所获得的利润为y元.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 若每天销售该商品要获得280元的利润,每件商品的售价应定为多少元?
若每天销售该商品要获得280元的利润,每件商品的售价应定为多少元?
![]() 求商店每天销售该商品可获得的最大利润.
求商店每天销售该商品可获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正三角形和正方形内接于同一个圆;如图②,正方形和正五边形内接于同一个圆;如图③,正五边形和正六边形内接于同一个圆;…;则对于图①来说,BD可以看作是正_____边形的边长;若正n边形和正(n+1)边形内接于同一个圆,连接与公共顶点相邻同侧两个不同正多边形的顶点可以看做是_____边形的边长.
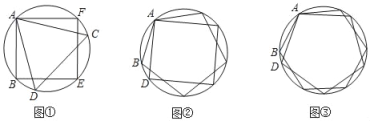
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,图象经过B(﹣3,0)、C(0,3)两点,且与x轴交于点A.
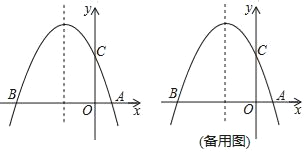
(1)求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)在抛物线的对称轴上找一点M,使△ACM周长最短,求出点M的坐标;
(3)若点P为抛物线对称轴上的一个动点,直接写出使△BPC为直角三角形时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
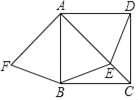
【题目】如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)BF和DE有怎样的数量关系?请证明你的结论;
(2)在其他条件都保持不变的是情况下,当点E运动到AC中点时,四边形AFBE是什么特殊四边形?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com