
����Ŀ���������һ�κ���y=k1x+b1��y=k2x+b2����k1=k2��b1��b2����ô��������һ�κ���Ϊ��ƽ��һ�κ���������ͼ����֪����y=-2x+4��ͼ����x�ᡢy��ֱ���A��B���㣬һ�κ���y=kx+b��y=-2x+4����ƽ��һ�κ�����
��1��������y=kx+b��ͼ����㣨3��1������b��ֵ��
��2��������y=kx+b��ͼ������������Χ�ɵ������κ���AOB����λ��ͼ�Σ�λ������Ϊԭ�㣬λ�Ʊ�Ϊ1��2������y=kx+b�ı���ʽ��
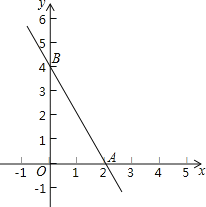
���𰸡�������
��������
���⣨1������ƽ��һ�κ����Ķ����֪��k=��2�������ô���ϵ�������b��ֵ���ɣ�
��2������λ�Ʊ�Ϊ1��2��֪������y=kx+b��������Ľ������꣬�����ô���ϵ�����������y=kx+b�ı���ʽ��
�����������1������֪�ã�k=��2���ѵ㣨3��1����k=��2����y=kx+b�еã�1=��2��3+b����b=7��
��2������λ�Ʊ�Ϊ1��2�ã�����y=kx+b��ͼ�������������
����������������ʱ������1��0���ͣ�0��2������ʱ����ʾΪ��y=��2x+2��
����������һ����ʱ��������1��0���ͣ�0����2������ʱ����ʾΪ��y=��2x��2��
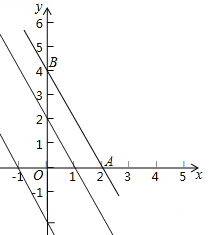



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x����1��ͼ��B����3��0����C��0��3�����㣬����x�ύ�ڵ�A��
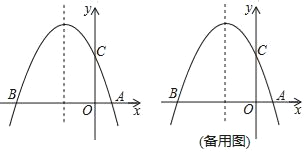
��1������κ���y��ax2+bx+c��a��0���ı���ʽ��
��2���������ߵĶԳ�������һ��M��ʹ��ACM�ܳ���̣������M�����ꣻ
��3������PΪ�����߶Գ����ϵ�һ�����㣬ֱ��д��ʹ��BPCΪֱ��������ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
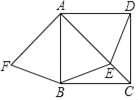
����Ŀ����ͼ��������ABCD������E��AC�ϣ�AF��AC������ΪA��AF��AE��
��1��BF��DE��������������ϵ����֤����Ľ��ۣ�
��2�����������������ֲ����������£�����E�˶���AC�е�ʱ���ı���AFBE��ʲô�����ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
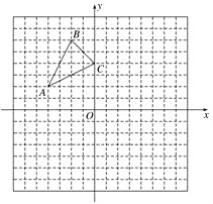
����Ŀ����ͼ����֪A(��4,2)��B(��2,6)��C(0,4)��ֱ������ϵƽ�������㣮
(1)����ABC����ƽ��4����λ������ƽ��1����λ���õ���A1B1C1������ƽ�ƺ��ͼ�Σ�
(2)����ABC�ڲ���һ��P(a��b)����ƽ�ƺ����Ķ�Ӧ��P1������Ϊ__________��
(3)��ԭ��OΪλ�����ģ�����ABC��СΪԭ����һ�룬�õ���A2B2C2����������������ϵ��������������������ͼ�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
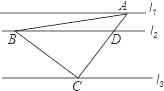
����Ŀ����ͼ��ֱ��l1��l2��l3��һ����ֱ��������ABC����������A��B��C�ֱ���l1��l2��l3�ϣ���ACB=90����AC��l2�ڵ�D����֪l1��l2�ľ���Ϊ1��l2��l3�ľ���Ϊ3����![]() ��ֵΪ�� ��
��ֵΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
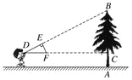
����Ŀ����ͼ��С��ͬѧ�����Ƶ�ֱ��������ֽ��DEF�������ĸ߶�AB���������Լ���λ�ã��跨ʹб��DF����ˮƽ�����ұ�DE���B��ͬһֱ���ϣ���ֽ֪�������ֱ�DZ�DE��50 cm��EF��25 cm����ñ�DF�����ĸ߶�AC��1.6 m��CD��10 m��������AB����(����)
A. 4 m
B. 5 m
C. 6.6 m
D. 7.7 m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
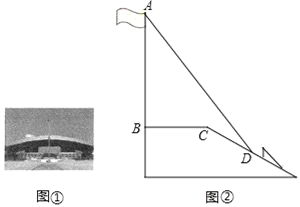
����Ŀ�������������Ĺ㳡���������ͼ����ʾ��ijѧУ��ȤС������˸���˵ĸ߶ȣ���ͼ�ڣ�ijһʱ�̣����AB��Ӱ��һ��������ƽ̨�ϣ���һ��������б���ϣ��������ƽ̨�ϵ�Ӱ��BCΪ16�ף�����б���ϵ�Ӱ��CDΪ8�ף�AB��BC��ͬһʱ�̣�̫��������ˮƽ��ļн�Ϊ45��.1�ı��EF������б���ϵ�Ӱ��FGΪ2�ף�����˵ĸ߶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�k��2��2x2+��2k+1��x+1��0��ʵ���⣬�ҷ���������y��![]() ��ͼ���ڶ��������ޣ���k�dz�������k��ֵΪ��������
��ͼ���ڶ��������ޣ���k�dz�������k��ֵΪ��������
A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�տ����������һ���Ϊ����ABCD��С�ݣ�AB+BC=10m��˩סС����10m��������һ�˹̶���B�㴦��С���ڲ��ܽ���С���ڵ������»������Ի���������ΪS��m2��.
��1����ͼ1����BC=4m����S=_____m2��
��2����ͼ2���ֿ����ڣ�1���о���ABCDС�ݵ��Ҳ���CDΪ����չһ����CDE����ʹ֮������Ϊ�����ABCED��С�ݣ������������䣬����BC�ı仯�����У���Sȡ����Сֵʱ����BC�ij�Ϊ____m��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com