
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m,拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
(1)如图1,若BC=4m,则S=_____m2.
(2)如图2,现考虑在(1)中矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其他条件不变,则在BC的变化过程中,当S取得最小值时,边BC的长为____m.

【答案】88π; ![]()
【解析】
(1)小狗活动的区域面积为以B为圆心、10m为半径的![]() 圆,以C为圆心、6m为半径的
圆,以C为圆心、6m为半径的![]() 圆和以A为圆心、4为半径的
圆和以A为圆心、4为半径的![]() 圆的面积和,据此列式求解可得;
圆的面积和,据此列式求解可得;
(2)此时小狗活动的区域面积为以B为圆心、10为半径的![]() 圆,以A为圆心、x为半径的
圆,以A为圆心、x为半径的![]() 圆、以C为圆心、10-x为半径的
圆、以C为圆心、10-x为半径的![]() 圆的面积和,列出函数解析式,由二次函数的性质解答即可.
圆的面积和,列出函数解析式,由二次函数的性质解答即可.
解:(1)如图,拴住小狗的10m长的绳子一端固定在B点处,小狗可以活动的区域如图所示:
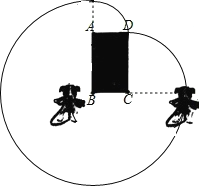
由图可知,小狗活动的区域面积为以B为圆心、10m为半径的![]() 圆,以C为圆心、6m为半径的
圆,以C为圆心、6m为半径的![]() 圆和以A为圆心、4m为半径的
圆和以A为圆心、4m为半径的![]() 圆的面积和,
圆的面积和,
∴S=![]() ×π102+
×π102+![]() π62+
π62+![]() π42=88π;
π42=88π;
(2)如图,
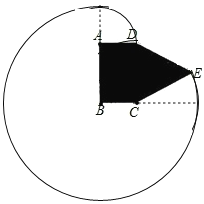
设BC=x,则AB=10-x,
∴S=![]() π102+
π102+![]() πx2+
πx2+![]() π(10-x)2
π(10-x)2
=![]() (x2-5x+250)
(x2-5x+250)
=![]() (x-
(x-![]() )2+
)2+![]() ,
,
当x=![]() 时,S取得最小值,
时,S取得最小值,
∴BC=![]() .
.
故答案为:(1)88π;(2)![]() .
.


科目:初中数学 来源: 题型:
【题目】如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.如图,已知函数y=-2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=-2x+4是“平行一次函数”
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形,位似中心为原点,位似比为1:2,求函数y=kx+b的表达式.
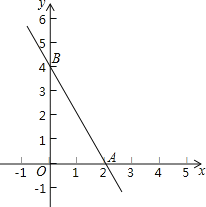
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,m)在双曲线y=![]() 上且m<0,过点A作x轴的垂线,垂足为B.
上且m<0,过点A作x轴的垂线,垂足为B.
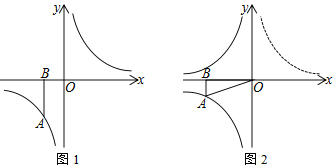
(1)如图1,当a=﹣2时,P(t,0)是x轴上的动点,将点B绕点P顺时针旋转90°至点C,
①若t=1,直接写出点C的坐标;
②若双曲线y=![]() 经过点C,求t的值.
经过点C,求t的值.
(2)如图2,将图1中的双曲线y=![]() (x>0)沿y轴折叠得到双曲线y=﹣
(x>0)沿y轴折叠得到双曲线y=﹣![]() (x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣
(x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣![]() (x<0)上的点D(d,n)处,求m和n的数量关系.
(x<0)上的点D(d,n)处,求m和n的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“富春包子”是扬州特色早点,富春茶社为了了解顾客对各种早点的喜爱情况,设计了如右图的调查问卷,对顾客进行了抽样调查.根据统计数据绘制了如下尚不完整的统计图.
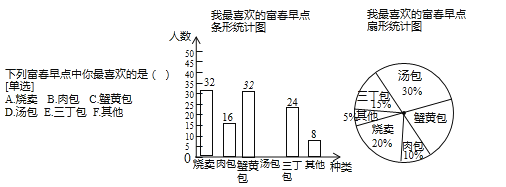
根据以上信息,解决下列问题:
(1)条形统计图中“汤包”的人数是 ,扇形统计图中“蟹黄包”部分的圆心角为 °;
(2)根据抽样调查结果,请你估计富春茶社1000名顾客中喜欢“汤包”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
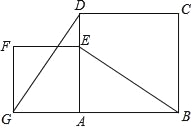
【题目】将边长为2![]() 的正方形ABCD与边长为2的正方形AEFG如图放置,AD与AE在同一直线上,AB与AG在同一直线上,连接DG、BE.
的正方形ABCD与边长为2的正方形AEFG如图放置,AD与AE在同一直线上,AB与AG在同一直线上,连接DG、BE.
(1)求证:DG=BE;
(2)把正方形AEFG绕点A旋转,当点F恰好落在AB边所在的直线上时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
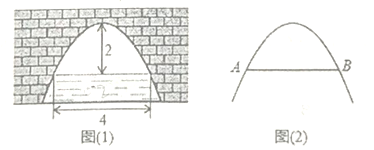
【题目】如图(1)是一个横断面为抛物线形状的拱桥,当水面宽![]() 为
为![]() 时,拱顶与水面距离为
时,拱顶与水面距离为![]() .
.
(1)请你在图(2)中,建立适当的平面直角坐标系,使该抛物线拱桥的函数关系式符合![]() 形式,并求此时,函数关系式;
形式,并求此时,函数关系式;
(2)当水面上升![]() 时,求水面宽度.
时,求水面宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若![]() .
.
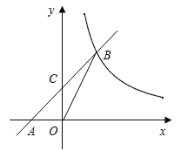
(1)求该反比例函数的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
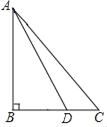
【题目】在△ABC中,∠B=90°,AB=BC,点D是BC边上的一点,连接AD,将AD绕点D顺时针旋转90°得到DE,作EF⊥BC交BC的延长线于点F.
(1)依题意补全图形;
(2)求证:EF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
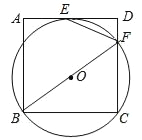
【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点E,与CD相交于点F,连接EF.
(1)求证:EF平分∠BFD.
(2)若tan∠FBC=![]() ,DF=
,DF=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com