
【题目】已知点A(a,m)在双曲线y=![]() 上且m<0,过点A作x轴的垂线,垂足为B.
上且m<0,过点A作x轴的垂线,垂足为B.
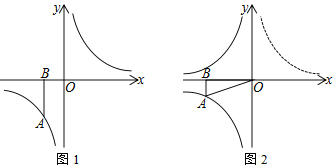
(1)如图1,当a=﹣2时,P(t,0)是x轴上的动点,将点B绕点P顺时针旋转90°至点C,
①若t=1,直接写出点C的坐标;
②若双曲线y=![]() 经过点C,求t的值.
经过点C,求t的值.
(2)如图2,将图1中的双曲线y=![]() (x>0)沿y轴折叠得到双曲线y=﹣
(x>0)沿y轴折叠得到双曲线y=﹣![]() (x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣
(x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣![]() (x<0)上的点D(d,n)处,求m和n的数量关系.
(x<0)上的点D(d,n)处,求m和n的数量关系.
【答案】(1)①C(1,3).②t=﹣4 或2;(2)满足条件的m、n的关系是m+n=0或mn=﹣8.
【解析】(1)①如图1﹣1中,求出PB、PC的长即可解决问题;
②图1﹣2中,由题意C(t,t+2),理由待定系数法,把问题转化为方程解决即可;
(2)分两种情形①当点A与点D关于x轴对称时,A(a,m),D(d,n),可得m+n=0.
②当点A绕点O旋转90°时,得到D′,D′在y=﹣![]() 上,作D′H⊥y轴,则△ABO≌△D′HO,推出OB=OH,AB=D′H,由A(a,m),推出D′(m,﹣a),即D′(m,n),由D′在y=﹣
上,作D′H⊥y轴,则△ABO≌△D′HO,推出OB=OH,AB=D′H,由A(a,m),推出D′(m,﹣a),即D′(m,n),由D′在y=﹣![]() 上,可得mn=﹣8.
上,可得mn=﹣8.
(1)①如图1﹣1中,

由题意:B(﹣2,0),P(1,0),PB=PC=3,
∴C(1,3);
②图1﹣2中,由题意C(t,t+2),

∵点C在y=![]() 上,
上,
∴t(t+2)=8,
∴t=﹣4 或2;
(2)如图2中,
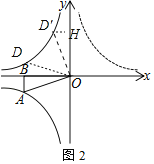
①当点A与点D关于x轴对称时,A(a,m),D(d,n),
∴m+n=0;
②当点A绕点O旋转90°时,得到D′,D′在y=﹣![]() 上,
上,
作D′H⊥y轴,则△ABO≌△D′HO,
∴OB=OH,AB=D′H,
∵A(a,m),
∴D′(m,﹣a),即D′(m,n),
∵D′在y=﹣![]() 上,
上,
∴mn=﹣8,
综上所述,满足条件的m、n的关系是m+n=0或mn=﹣8.


科目:初中数学 来源: 题型:
【题目】先尺规作图,后进行计算:如图,△ABC中,∠A=105°.
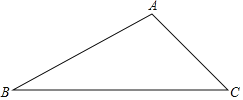
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到∠ABC两边的距离相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ACP=30°,则∠PBC的度数为 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用1块A型钢板可制成2块C型钢板和1块D型钢板;用1块B型钢板可制成1块C型钢板和3块D型钢板.现准备购买A、B型钢板共100块,并全部加工成C、D型钢板.要求C型钢板不少于120块,D型钢板不少于250块,设购买A型钢板x块(x为整数).
(1)求A、B型钢板的购买方案共有多少种?
(2)出售C型钢板每块利润为100元,D型钢板每块利润为120元.若将C、D型钢板全部出售,请你设计获利最大的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了 h;
(2)求线段DE对应的函数解析式;
(3)求轿车从甲地出发后经过多长时间追上货车.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.
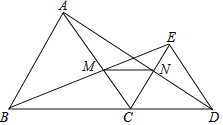
(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:△MNC是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用一根12米长的木材做一个中间有一条横档的日字形窗户.设AB=x米.
(1)用含有x的代数式表示线段AC的长.
(2)若使透进窗户的光线达到6平方米,则窗户的长和宽各为多少?
(3)透进窗户的光线能达到9平方米吗?若能,请求出这个窗户的长和宽;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
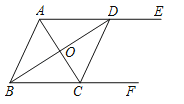
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com