
【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,
组别 | 课堂发言次数n |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
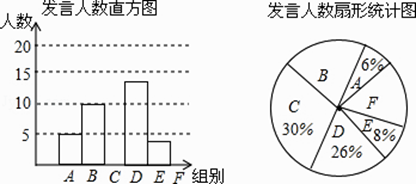
请结合图中相关数据回答下列问题:
(1)样本容量是 , 并补全直方图;
(2)该年级共有学生800人,请估计该年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰好有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好都是男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况 (超产记为正,减产记为负):

(1) 写出该厂星期一生产工艺品的数量.
(2) 本周产量最多的一天比最少的一天多生产多少个工艺品?
(3) 请求出该工艺品厂在本周实际生产工艺品的数量.
(4) 已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个可得50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国宋朝数学家杨辉在他的著作![]() 详解九章算法
详解九章算法![]() 中提出“杨辉三角”
中提出“杨辉三角”![]() 如图
如图![]() ,此图揭示了
,此图揭示了![]() 为非负整数
为非负整数![]() 展开式的项数及各项系数的有关规律.
展开式的项数及各项系数的有关规律.
例如:![]() ,它只有一项,系数为1;系数和为1;
,它只有一项,系数为1;系数和为1;
![]() ,它有两项,系数分别为1,1,系数和为2;
,它有两项,系数分别为1,1,系数和为2;
![]() ,它有三项,系数分别为1,2,1,系数和为4;
,它有三项,系数分别为1,2,1,系数和为4;
![]() ,它有四项,系数分别为1,3,3,1,系数和为8;
,它有四项,系数分别为1,3,3,1,系数和为8;![]() ,
,
则![]() 的展开式共有______项,系数和为______.
的展开式共有______项,系数和为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在数轴上A点表示数![]() ,B点表示数
,B点表示数![]() ,且
,且![]() 、
、![]() 满足
满足![]() ,
,
![]()
(1)点A表示的数为_______;点B表示的数为__________;
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=3BC,则C点表示的数__________;
(3)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请分别表示出甲、乙两小球到原点的距离(用含t的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“算经十书”是指汉唐一千多年间的十部著名数学著作,它们曾经是隋唐时期国子监算学科的教科书,这些流传下来的古算书中凝聚着历代数学家的劳动成果.下列四部著作中,不属于我国古代数学著作的是( )
A.  《九章算术》 B.
《九章算术》 B.  《几何原本》
《几何原本》
C.  《海岛算经》 D.
《海岛算经》 D.  《周髀算经》
《周髀算经》
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE .
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE . 
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y= ![]() x+b过点D与线段AB交于点F,延长OF交反比例函数y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y= ![]() (x<0)的图象于点N,求N点坐标.
(x<0)的图象于点N,求N点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com