
【题目】如图,正方形AOCB的边长为4,反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE .
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE . 
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y= ![]() x+b过点D与线段AB交于点F,延长OF交反比例函数y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y= ![]() (x<0)的图象于点N,求N点坐标.
(x<0)的图象于点N,求N点坐标.
【答案】
(1)解:∵S△AOE=3S△OBE,
∴AE=3BE,
∴AE=3,
∴E(﹣3,4)
反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,
(k≠0,且k为常数)的图象过点E,
∴4= ![]() ,即k=﹣12
,即k=﹣12
(2)解:∵正方形AOCB的边长为4,
∴点D的横坐标为﹣4,点F的纵坐标为4.
∵点D在反比例函数的图象上,
∴点D的纵坐标为3,即D(﹣4,3).
∵点D在直线y= ![]() x+b上,
x+b上,
∴3= ![]() ×(﹣4)+b,解得b=5.
×(﹣4)+b,解得b=5.
∴直线DF为y= ![]() x+5,
x+5,
将y=4代入y= ![]() x+5,得4=
x+5,得4= ![]() x+5,解得x=﹣2.
x+5,解得x=﹣2.
∴点F的坐标为(﹣2,4),
设直线OF的解析式为y=mx,
代入F的坐标得,4=﹣2m,
解得m=﹣2,
∴直线OF的解析式为y=﹣2x,
解  ,得
,得 ![]() .
.
∴N(﹣ ![]() ,2
,2 ![]() ).
).
【解析】(1)根据题意求得E的坐标,把点E(﹣3,4)代入利用待定系数法即可求出k的值;(2)由正方形AOCB的边长为4,故可知点D的横坐标为﹣4,点F的纵坐标为4.由于点D在反比例函数的图象上,所以点D的纵坐标为3,即D(﹣4,3),由点D在直线y= ![]() x+b上可得出b的值,进而得出该直线的解析式,再把y=4代入直线的解析式即可求出点F的坐标,然后根据待定系数法求得直线OF的解析式,然后联立方程解方程组即可求得.
x+b上可得出b的值,进而得出该直线的解析式,再把y=4代入直线的解析式即可求出点F的坐标,然后根据待定系数法求得直线OF的解析式,然后联立方程解方程组即可求得.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
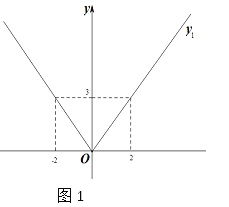
【题目】(1)写出图1中函数图象的解析式y1=_________________.
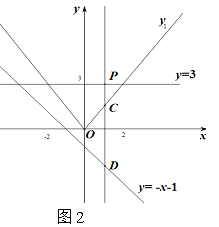
(2)如图2,过直线y=3上一点P(m,3)作x轴的垂线交y1的图象于点C,交y= -x- 1于点D.
①当m>0时,试比较PC与PD的大小,并证明你的结论.
②若CD<3时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
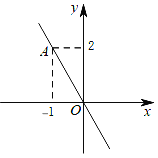
【题目】已知:如图,正比例函数y=kx的图象经过点A,
(1)请你求出该正比例函数的解析式;
(2)若这个函数的图象还经过点B(m,m+3),请你求出m的值;
(3)请你判断点P(﹣![]() ,1)是否在这个函数的图象上,为什么?
,1)是否在这个函数的图象上,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1 , 还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2017次操作后得到的折痕D2016E2016 , 到BC的距离记为h2017;若h1=1,则h2017的值为 . 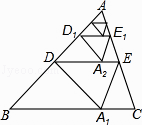
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°,F是AC的中点,过AC上一点D作DE//AB,交BF的延长线于点E,AG⊥BE,垂足是G,连接BD、AE.
(1)求证:△ABC∽△BGA;
(2)若AF=5,AB=8,求FG的长;
(3)当AB=BC,∠DBC=30°时,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y= ![]() (x>0)的图象经过顶点B,则反比例函数的表达式为( )
(x>0)的图象经过顶点B,则反比例函数的表达式为( ) 
A.y= ![]()
B.y= ![]()
C.y= ![]()
D.y= ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com