
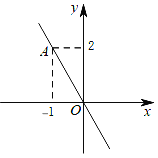
【题目】已知:如图,正比例函数y=kx的图象经过点A,
(1)请你求出该正比例函数的解析式;
(2)若这个函数的图象还经过点B(m,m+3),请你求出m的值;
(3)请你判断点P(﹣![]() ,1)是否在这个函数的图象上,为什么?
,1)是否在这个函数的图象上,为什么?
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】某工艺品厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况 (超产记为正,减产记为负):

(1) 写出该厂星期一生产工艺品的数量.
(2) 本周产量最多的一天比最少的一天多生产多少个工艺品?
(3) 请求出该工艺品厂在本周实际生产工艺品的数量.
(4) 已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个可得50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节约意识,我市出台阶梯电价计算方案:居民生活用电将月用电量分为三档,第一档为月用电量200度(含)以内,第二档为月用电量200~320度(含),第三档为月用电量320度以上.这三个档次的电价分别为:第一档0.52元/度,第二档0.57元/度,第三档0.82元/度.
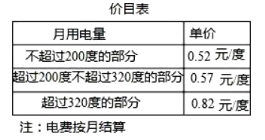
(1)若某户居民10月份电费78元,则该户居民10月份用电________度;
(2)若该户居民2月份用电340度,则应缴电费________元;
(3)用x(度)来表示月用电量,请根据x的不同取值范围,用含x的代数式表示出月用电费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
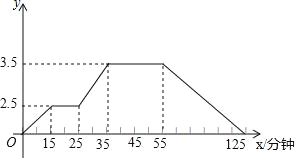
【题目】如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.
(1)体育场离小强家有多远?小强从家到体育场用了多长时间?
(2)体育场距文具店多远?
(3)小强在文具店逗留了多长时间?
(4)小强从文具店回家的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE .
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE . 
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y= ![]() x+b过点D与线段AB交于点F,延长OF交反比例函数y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y= ![]() (x<0)的图象于点N,求N点坐标.
(x<0)的图象于点N,求N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A,B,C,表示的数分别是﹣4,﹣2,3.
![]()
(1)若使C、B两点的距离是A、B两点的距离的2倍,则需将点C向左移动 个单位;
(2)点A、B、C开始在数轴上运动,若点A以每秒a个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,设运动时间为t秒:
①点A、B、C表示的数分别是 、 、 (用含a、t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2,当a为何值时,5d1﹣3d2的值不会随着时间t的变化而改变,并求此时5d1﹣3d2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
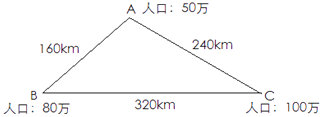
【题目】据有关资料统计,两个城市之间每天的电话通话次数T与这两个城市的人口数xy(单位:万人)以及两城市间的距离l(单位:km)之间有下列关系式![]() (k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)
(k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com