
【题目】为了加强公民的节约意识,我市出台阶梯电价计算方案:居民生活用电将月用电量分为三档,第一档为月用电量200度(含)以内,第二档为月用电量200~320度(含),第三档为月用电量320度以上.这三个档次的电价分别为:第一档0.52元/度,第二档0.57元/度,第三档0.82元/度.
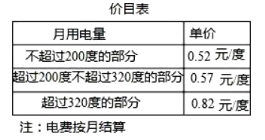
(1)若某户居民10月份电费78元,则该户居民10月份用电________度;
(2)若该户居民2月份用电340度,则应缴电费________元;
(3)用x(度)来表示月用电量,请根据x的不同取值范围,用含x的代数式表示出月用电费用.
【答案】(1)150;(2)188.8;(3)见解析.
【解析】
(1)根据题意可知该户居民10月份用电少于200度,应缴纳电费为:度数×0.52;
(2)根据应缴纳电费为:200×0.52+超过200度的度数不超过320度的度数×0.57+超过320度的度数×0.82,列式计算即可求解;
(3)分三种情况讨论即可求解.
(1)∵0.52×200=104>78,
∴该户居民10月份用电少于200度,
设该户居民10月份用电x度,依题意有:
0.52x=78,
解得x=150,
故该户居民10月份用电150度,
故答案为:150;
(2)若该户居民2月份用电340度,则应缴电费:
200×0.52+(320-200)×0.57+(340-320)×0.82,
=104+68.4+16.4,
=188.8(元),
故答案为:188.8;
(3)当月用电量在200度(含)以内,电费为0.52x元;
当月用电量在200~320度(含)范围,电费为0.52×200+0.57(x-200)=(0.57x-10)元;
当月用电量在320度以上时,电费为0.52×200+0.57×120+0.82(x-320)=(0.82x-90)元.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
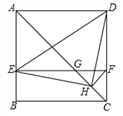
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作![]() ,与AC、DC分别交于点
,与AC、DC分别交于点![]() 为CG的中点,连结DE、EH、DH、
为CG的中点,连结DE、EH、DH、![]() 下列结论:
下列结论: ![]() ;
; ![]() ≌
≌![]() ;
; ![]() ;
; ![]() 若
若![]() ,则
,则![]() 其中结论正确的有
其中结论正确的有![]()
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线l1 , l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2 , 经过点A、B、C的抛物线的对称轴与直线l1交于点K,如图所示.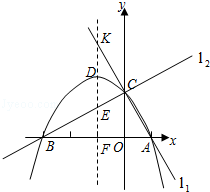
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1 , 抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
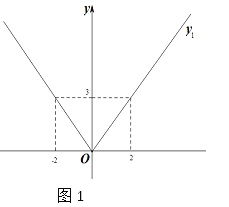
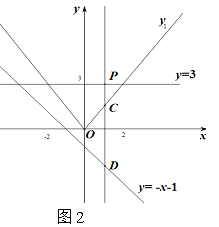
【题目】(1)写出图1中函数图象的解析式y1=_________________.
(2)如图2,过直线y=3上一点P(m,3)作x轴的垂线交y1的图象于点C,交y= -x- 1于点D.
①当m>0时,试比较PC与PD的大小,并证明你的结论.
②若CD<3时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
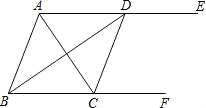
【题目】如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,AC=6,求AE,BF之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
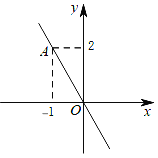
【题目】已知:如图,正比例函数y=kx的图象经过点A,
(1)请你求出该正比例函数的解析式;
(2)若这个函数的图象还经过点B(m,m+3),请你求出m的值;
(3)请你判断点P(﹣![]() ,1)是否在这个函数的图象上,为什么?
,1)是否在这个函数的图象上,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°,F是AC的中点,过AC上一点D作DE//AB,交BF的延长线于点E,AG⊥BE,垂足是G,连接BD、AE.
(1)求证:△ABC∽△BGA;
(2)若AF=5,AB=8,求FG的长;
(3)当AB=BC,∠DBC=30°时,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由相同的花盆按一定的规律组成的正多边形图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,![]() ,则第8个图形中花盆的个数为( )
,则第8个图形中花盆的个数为( )

A. 90 B. 64 C. 72 D. 56
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com