
【题目】如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.
(1)体育场离小强家有多远?小强从家到体育场用了多长时间?
(2)体育场距文具店多远?
(3)小强在文具店逗留了多长时间?
(4)小强从文具店回家的平均速度是多少?
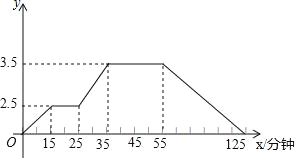
【答案】(1)体育场离陈欢家2.5千米,小刚在体育场锻炼了15分钟;(2)体育场离文具店1千米;(3)小刚在文具店停留20分;(4)小强从文具店回家的平均速度是![]() 千米/分
千米/分
【解析】
(1)根据观察函数图象的纵坐标,可得距离,观察函数图象的横坐标,可得时间;
(2)根据观察函数图象的横坐标,可得体育场与文具店的距离;
(3)观察函数图象的横坐标,可得在文具店停留的时间;
(4)用回家的路程除以回家的时间即可.
(1)由纵坐标看出体育场离陈欢家2.5千米,由横坐标看出小刚在体育场锻炼了15分钟;
(2)由纵坐标看出体育场离文具店3.5-2.5=1(千米);
(3)由横坐标看出小刚在文具店停留55-35=20(分);
(4)小强从文具店回家的平均速度是3.5÷(125-55)=![]() (千米/分)
(千米/分)


科目:初中数学 来源: 题型:
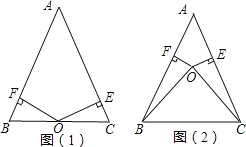
【题目】已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
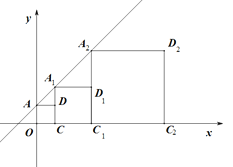
【题目】如图,正方形AOCD、正方形A1CC1D1、正方形A2C1C2D2的顶点A、A1、A2和O、C、C1、C2分别在一次函数y=x+1的图象和x轴上,若正比例函数y=kx则过点D5,则系数k的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
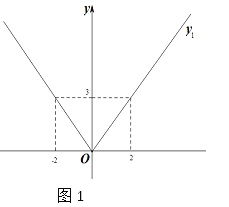
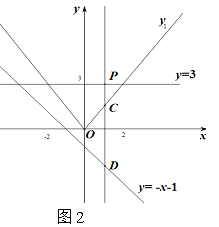
【题目】(1)写出图1中函数图象的解析式y1=_________________.
(2)如图2,过直线y=3上一点P(m,3)作x轴的垂线交y1的图象于点C,交y= -x- 1于点D.
①当m>0时,试比较PC与PD的大小,并证明你的结论.
②若CD<3时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
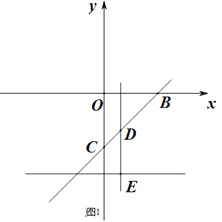
【题目】已知点C(0,-2),直线l:y=kx-2k无论k取何值,直线总过定点B,
(1)求定点B的坐标.
(2)如图1,若点D为直线BC上(点(-1,-3)除外)一动点,过点D作x轴的垂线交y= - 3于点E,点F在直线BC上,距离D点为![]() 个单位,D点横坐标为t,ΔDEF的面积为S,求S与t函数关系式.
个单位,D点横坐标为t,ΔDEF的面积为S,求S与t函数关系式.
(3)若直线BC关于x轴对称后再向上平移5个单位得到直线B1C1,如图2,点G(1,a)和H(6,b)是直线B1C1上两点,点P(m,n)为第一象限内(G、H两点除外)的一点,,且mn=6,直线PG和PH为分别交y轴于点MN两点,问线段OM、ON有什么数量关系,请证明.
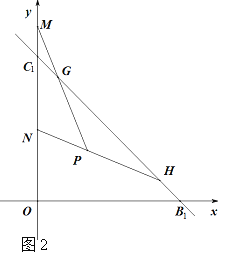
查看答案和解析>>
科目:初中数学 来源: 题型:
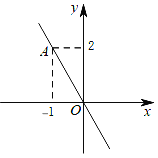
【题目】已知:如图,正比例函数y=kx的图象经过点A,
(1)请你求出该正比例函数的解析式;
(2)若这个函数的图象还经过点B(m,m+3),请你求出m的值;
(3)请你判断点P(﹣![]() ,1)是否在这个函数的图象上,为什么?
,1)是否在这个函数的图象上,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1 , 还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2017次操作后得到的折痕D2016E2016 , 到BC的距离记为h2017;若h1=1,则h2017的值为 . 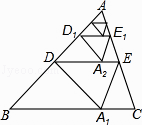
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料: 如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)根据以上材料解决下列问题: 如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= ![]() .
.
①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com