
����Ŀ����ͼ����������������A��B��C����ʾ�����ֱ��ǩ�4����2��3��
![]()
��1����ʹC��B����ľ�����A��B����ľ����2�������轫��C�����ƶ��� ������λ��
��2����A��B��C��ʼ���������˶�������A��ÿ��a����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶������˶�ʱ��Ϊt�룺
����A��B��C��ʾ�����ֱ����� ������ ������ �������ú�a��t�Ĵ���ʽ��ʾ����
������B���C֮��ľ����ʾΪd1����A���B֮��ľ����ʾΪd2����aΪ��ֵʱ��5d1��3d2��ֵ��������ʱ��t�ı仯���ı䣬�����ʱ5d1��3d2��ֵ��
���𰸡���1��1��10��2������4��at����2+2t��3+5t��19
��������
��1����AB=2��������ἴ�ɵó���C�����ƶ��ľ��룻
��2���ٽ��·��=ʱ�����ٶ�д���𰸣�
�������d1=3t+5��d2=��a+2��t+2���Ӷ��ó�5d1��3d2=��9��3a��t+19��
��1���������֪��A��B����ľ���Ϊ2��B�㡢C���ʾ�����ֱ�Ϊ����2��3��
���Ե�C��B����ľ�����A��B����ľ����2��ʱ���轫��C�����ƶ�1��10����λ��
�ʴ��ǣ�1��10��
��2���ٵ�A��ʾ�����ǩ�4��at����B��ʾ�����ǩ�2+2t����C����ʾ������3+5t��
�ʴ��ǣ���4��at����2+2t��3+5t��
�ڡߵ�A��ÿ��a����λ���ٶ������˶�����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶���
��d1=3t+5��d2=��a+2��t+2��
��5d1��3d2=5��3t+5����3[��a+2��t+2]=��9��3a��t+19��
9��3a=0��
���a=3��
�ʵ�aΪ3ʱ��5d1��3d2��ֵ��������ʱ��t�ı仯���ı䣬��ʱ5d1��3d2��ֵΪ19��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У�E��CA�ӳ����ϵĵ㣬F��AC�ӳ����ϵĵ㣬��AE=CF����֤��
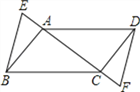
��1����ABE�ա�CDF��
��2��BE��DF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
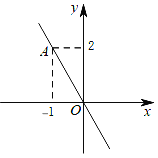
����Ŀ����֪����ͼ������������y=kx��ͼ����A��
��1����������������������Ľ���ʽ��
��2�������������ͼ������B��m��m+3�����������m��ֵ��
��3�������жϵ�P����![]() ��1���Ƿ������������ͼ���ϣ�Ϊʲô��
��1���Ƿ������������ͼ���ϣ�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ABC=90�㣬F��AC���е㣬��AC��һ��D��DE//AB����BF���ӳ����ڵ�E��AG��BE��������G������BD��AE��
��1����֤����ABC�ס�BGA��
��2����AF=5��AB=8����FG�ij���
��3����AB=BC����DBC=30��ʱ���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��![]() ��ƽ�����ཻ�ڵ�E������E��
��ƽ�����ཻ�ڵ�E������E��![]() ��
��![]() �ڵ�F����ôEF�ij�Ϊ�� ��
�ڵ�F����ôEF�ij�Ϊ�� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. ��2��x+1��=x+7ȥ���š�����ϲ�ͬ�����x=5
B. ��![]() =1+
=1+![]() ȥ��ĸ����2��2x��1��=1+3��x��3��
ȥ��ĸ����2��2x��1��=1+3��x��3��
C. ��2��2x��1����3��x��3��=1ȥ���ţ���4x��2��3x��9=1
D. ��7x=4x��3�����7x��4x=3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�CD��AB�ڵ�D��CE�ǡ�ACB��ƽ���ߣ���A��20��,��B��60�������BCD�͡�ECD�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ͬ�Ļ��谴һ���Ĺ�����ɵ��������ͼ�������е�1��ͼ��һ����6�����裬��2��ͼ��һ����12�����裬��3��ͼ��һ����20�����裬![]() �����8��ͼ���л���ĸ���Ϊ�� ��
�����8��ͼ���л���ĸ���Ϊ�� ��

A. 90 B. 64 C. 72 D. 56
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����塱��ji��ng����һ��������������дʣ���һ���������Ƶ����飮��ͼ��ʾ��һ�ű߳�Ϊ8cm�������ε�ֽƬ����ȥ����һ����Сֱ�������κ�һ�������εõ�һ����������ͼ��(��Ӱ����).���ȥ��С�����γ��Ϳ��ֱ�Ϊxcm��ycm����ȥ������Сֱ�������ε���ֱ�DZ߳�Ҳ�ֱ�Ϊxcm��ycm��

(1)�ú���x��y�Ĵ���ʽ��ʾͼ�С��塱����Ӱ���֣������.
(2)��x=8��y=2ʱ�����ʱ���塱����Ӱ���֣��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com