
【题目】如图,在△ABC中,CD⊥AB于点D,CE是∠ACB的平分线,∠A=20°,∠B=60°,求∠BCD和∠ECD的度数.

 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE .
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE . 
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y= ![]() x+b过点D与线段AB交于点F,延长OF交反比例函数y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y= ![]() (x<0)的图象于点N,求N点坐标.
(x<0)的图象于点N,求N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A,B,C,表示的数分别是﹣4,﹣2,3.
![]()
(1)若使C、B两点的距离是A、B两点的距离的2倍,则需将点C向左移动 个单位;
(2)点A、B、C开始在数轴上运动,若点A以每秒a个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,设运动时间为t秒:
①点A、B、C表示的数分别是 、 、 (用含a、t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2,当a为何值时,5d1﹣3d2的值不会随着时间t的变化而改变,并求此时5d1﹣3d2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
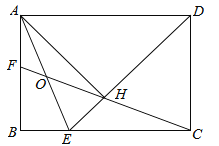
【题目】(3分)如图,在矩形ABCD中,BC=![]() AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
①∠AEB=∠AEH;②DH=![]() EH;③HO=
EH;③HO=![]() AE;④BC﹣BF=
AE;④BC﹣BF=![]() EH.
EH.
其中正确命题的序号是 (填上所有正确命题的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取一张矩形的纸片进行折叠,具体操作过程如下: 第一步:先把矩形ABCD对折,折痕为MN,如图(1);
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B′,得Rt△AB′E,如图(2);
第三步:沿EB′线折叠得折痕EF,如图(3).
若AB= ![]() ,则EF的值是( )
,则EF的值是( )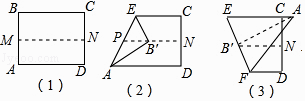
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
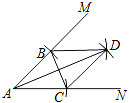
【题目】如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于![]() BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.若∠MBD=40°,则∠NCD的度数为_____.
BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.若∠MBD=40°,则∠NCD的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
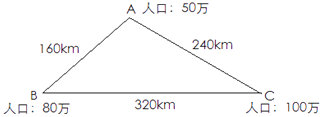
【题目】据有关资料统计,两个城市之间每天的电话通话次数T与这两个城市的人口数xy(单位:万人)以及两城市间的距离l(单位:km)之间有下列关系式![]() (k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)
(k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
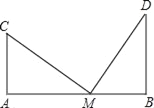
【题目】如图,两根旗杆AC与BD相距12m,某人从B点沿AB走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为0、5m/s,求这个人走了多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com