
����Ŀ����ͼ��������A���ʾ��![]() ��B���ʾ��
��B���ʾ��![]() ����
����![]() ��
��![]() ����
����![]() ��
��
![]()
��1����A��ʾ����Ϊ_______����B��ʾ����Ϊ__________;
��2������A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC��������������һ��C��ʹAC��3BC����C���ʾ����__________;
��3������ԭ��O����һ���壬һС��״ӵ�A����1����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�B����2����λ/����ٶ�Ҳ�����˶������������������Ĵ�С���ɿ���һ�㣩��ԭ�����ٶ����෴�ķ����˶������˶���ʱ��Ϊt���룩����ֱ��ʾ���ס�����С��ԭ��ľ��루�ú�t�Ĵ���ʽ��ʾ��
���𰸡���1��-5��7��2��4��13����3���ף�5+t���ң�0t3.5ʱ��72t����t>3.5ʱ��2t7
�������������������1�����ݷǸ����������з������a��b��ֵ���Ӷ��ý⣻��2��������������ı�ʾ�г�����ֵ���̣�Ȼ����⼴�ɣ���3����С����������ϵ����������ʾ���ɣ���С��������������ƶ��������ֱַ���ʽ��ʾ���ɣ�
���������(1)������ã�a+5=0��b7=0��
���a=5��b=7��
���ԣ���A��ʾ5����B��ʾ7��
(2)���C��ʾx��������ã�|5x|=3|7x|��
����,5+x=3(7x)��5+x=3(7x)��
���x=4����x=13��
���ԣ���C��ʾ����Ϊ4��13��
(3)�ף���С��״ӵ�A����1����λ/����ٶ������˶���
���ԭ��ľ���Ϊ|5t|=5+t��
��С���Ҵӵ�B����2����λ/����ٶ�Ҳ�����˶���
���ҵ���ԭ���ʱ��Ϊ7��2=3.5��
�൱0t3.5ʱ��С��ԭ��ľ���Ϊ72t��
��t>3.5ʱС��ԭ��ľ���Ϊ2t7.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����MON=45�㣬OA1=1����������A1B1C1A2 �� �ܳ�����C1�������ڶ���������A2B2C2A3 �� �ܳ�����C2��������������������A3B3C3A4 �� �ܳ�����C3����A1��A2��A3��A4��������ON�ϣ���B1��B2��B3��B4��������OM�ϣ����������ƣ����n�������ε��ܳ�Cn= �� 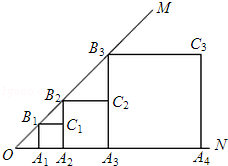
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
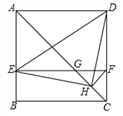
����Ŀ����ͼ����������ABCD�У�ACΪ�Խ��ߣ�EΪAB��һ�㣬����E��![]() ����AC��DC�ֱ��ڵ�
����AC��DC�ֱ��ڵ�![]() ΪCG���е㣬����DE��EH��DH��
ΪCG���е㣬����DE��EH��DH��![]() ���н��ۣ�
���н��ۣ� ![]() ��
�� ![]() ��
��![]() ��
�� ![]() ��
�� ![]() ��
��![]() ����
����![]() ���н�����ȷ����
���н�����ȷ����![]()
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
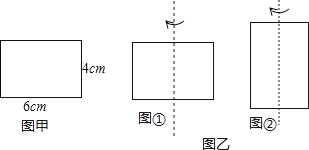
����Ŀ��̽������һ��6cm����4cm�ľ���ֽ�壬��Ҫ������һ��Ա��е�����ֱ��Ϊ�ᣬ��ת180�����õ�һ��Բ�����ֿɰ������ַ������в�����
����һ���Խϳ���һ��Ա��е�����ֱ��Ϊ����ת����ͼ�٣�
���������Խ϶̵�һ��Ա��е�����ֱ��Ϊ����ת����ͼ�ڣ�
��1����ͨ������˵�����ַ��������Բ�������
��2������þ��εij����ֱ���5cm��3cm�أ���ͨ������˵�����ַ��������Բ�������
��3��ͨ������̽�����㷢�ֶ���ͬһ�����Σ������������Σ�������һ��Ա��е�����ֱ��Ϊ����ת�õ�һ��Բ���������������õ���Բ���������˵��ԭ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˹��������Լ��ˮ�����÷ֽμƷѵķ������¼���ÿ����ͥ��ˮ�ѣ�����ˮ��������20m3ʱ����2Ԫ/m3���㣻����ˮ������20m3ʱ�����е�20m3��2Ԫ/m3���㣬�������ְ�2.6Ԫ/m3���㣮��ij����ͥ����ˮ��xm3��
�·� | 4�� | 5�� | 6�� |
��ˮ�� | 15 | 17 | 21 |
��1���ú�x��ʽ�ӱ�ʾ��
��0��x��20ʱ��ˮ��Ϊ�� ��Ԫ��
��x��20ʱ��ˮ��Ϊ�� ��Ԫ��
��2��С���ҵڶ�������ˮ������ϱ���С����������ȹ�����ˮ�Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AB=3��AD=4����ABC=60�㣬��BC���е�E��EF��AB������Ϊ��F����DC���ӳ����ཻ�ڵ�H�����DEF������� �� 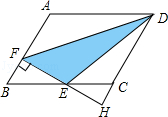
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У�E��CA�ӳ����ϵĵ㣬F��AC�ӳ����ϵĵ㣬��AE=CF����֤��
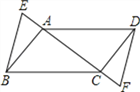
��1����ABE�ա�CDF��
��2��BE��DF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��l1 �� l2�ֱ���A��1��0������B����3��0�������ҵ���ֱ��ͬʱ�ཻ��y������ĵ�Cʱ��ǡ����l1��l2 �� ������A��B��C�������ߵĶԳ�����ֱ��l1���ڵ�K����ͼ��ʾ��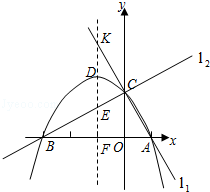
��1�����C�����꣬����������ߵĺ�������ʽ��
��2�������ߵĶԳ��ᱻֱ��l1 �� �����ߣ�ֱ��l2��x�����νص������߶Σ����������߶��к�������ϵ����˵�����ɣ�
��3����ֱ��l2�Ƶ�C��תʱ���������ߵ���һ������ΪM�����ҳ�ʹ��MCKΪ���������εĵ�M���������ɣ���д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ABC=90�㣬F��AC���е㣬��AC��һ��D��DE//AB����BF���ӳ����ڵ�E��AG��BE��������G������BD��AE��
��1����֤����ABC�ס�BGA��
��2����AF=5��AB=8����FG�ij���
��3����AB=BC����DBC=30��ʱ���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com