
����Ŀ�����������ӡ���������ɫ��㣬��������Ϊ���˽�˿ͶԸ�������ϲ����������������ͼ�ĵ����ʾ����Թ˿ͽ����˳������飮����ͳ�����ݻ����������в�������ͳ��ͼ��
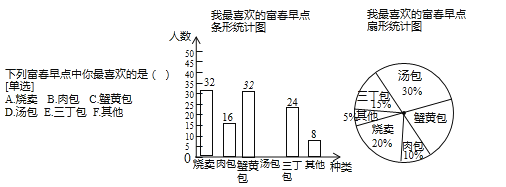
����������Ϣ������������⣺
��1������ͳ��ͼ�С��������������� ������ͳ��ͼ�С�з�ư������ֵ�Բ�Ľ�Ϊ �㣻
��2�����ݳ�����������������Ƹ�������1000���˿���ϲ�������������ж����ˣ�
���𰸡���1��48�ˣ�72����2��300��
�������������������1����ϲ����������������������ռ�İٷֱȼ���������������������ϲ������������ռ�İٷֱȳ������������������������������ϲ����з�ư������������Ե�������������ɵõ���ռ�İٷֱȣ��ٳ���360������������
��2���ù˿���ϲ������������ռ�İٷֱȣ�����1000���ɵõ������
�����������1��8��5%=160���ˣ���160��30%=48���ˣ���32��160��360��=0.2��360��=72�㣬
������ͳ��ͼ�С���������������48�ˣ�����ͳ��ͼ�С�з�ư������ֵ�Բ�Ľ�Ϊ72�㣬
�ʴ�Ϊ��48�ˣ�72��
��2��30%��1000=300���ˣ���
�ʹ��Ƹ�������1000���˿���ϲ��������������300�ˣ�


 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y= ![]() ��y=m��x��ͼ���һ��������A��2��3��������k��mΪ������
��y=m��x��ͼ���һ��������A��2��3��������k��mΪ������
��1����k��m��ֵ�����������IJ�ͼ��
��2������ͼ��ȷ���Ա���x��ȡֵ��Χ��ʹһ�κ����ĺ���ֵ���ڷ����������ĺ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��չ������μ�����Ҫ�����������������ɸ�����֪����2�������3��������Ҫ380Ԫ������4�������5��������Ҫ700Ԫ��
(1)����һ������һ������������Ԫ��
(2)��������ʦ����8000Ԫȥ������������������100�������������϶࣬����������һ�ɴ���ۡ����Żݼۣ���ô������ܹ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��ODǡΪ��BOE��ƽ���ߣ�
(1)ͼ�С�BOC�IJ����� �ѷ��������ĽǶ������)��
(2)����AOD��145�������AOE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ش��������⣺
(1)���㣺��(x��2)(x��3)�� ���� (x ��7)( x��10)�� ����(x��5)(x��6)�� ��
(2)�ܽṫʽ��(x��a)(x��b)�� ��
(3����֪a��b��m��Ϊ��������(x+a)(x+b)=x2+mx+6����m�����п���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AM��CN����BΪƽ����һ�㣬AB��BC��B��
��1����ͼ1��ֱ��д����A�͡�C֮���������ϵ________��
��2����ͼ2������B��BD��AM�ڵ�D����֤����ABD=��C��
��3����ͼ3���ڣ�2���ʵ������£���E��F��DM�ϣ�����BE��BF��CF��BFƽ�֡�DBC��BEƽ�֡�ABD������FCB+��NCF=180�㣬��BFC=3��DBE�����EBC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����A����D����EGC����FHB
��1����֤��AB��CD
��2����֤����E����F
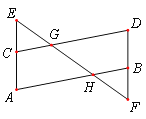
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC������OΪAC���ϵ�һ������������O��ֱ��MN��BC����MN����BCA�����ƽ����CF�ڵ�F������ACB�ڽ�ƽ����CE��E��

��1����֤��EO=FO��
��2������O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���֤����Ľ��ۣ�
��3����AC���ϴ��ڵ�O��ʹ�ı���AECF����������������ABC����״��֤����Ľ��ۡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���ABC+��D=180����ACƽ�֡�BAD��CE��AB��CF��AD����˵����
��1����CBE�ա�CDF��
��2��AB+DF=AF��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com