
【题目】如图,直线AB与CD相交于点O,OD恰为∠BOE的平分线.
(1)图中∠BOC的补角是 把符合条件的角都填出来);
(2)若∠AOD=145°,求∠AOE的度数.

科目:初中数学 来源: 题型:
【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点F是AD的中点,过点D作DE∥AC,交CF的延长线于点E,连接BE,AE.
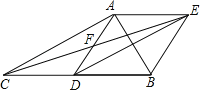
(1)求证:四边形ACDE是平行四边形;
(2)若AB=AC,试判断四边形ADBE的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
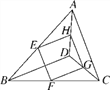
【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点,连接EF,FG,GH,HE.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
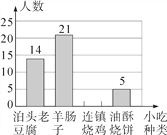
【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的沧州——我最喜爱的沧州小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:
调查问卷
在下面四种沧州小吃中,你最喜爱的是(____)(单选)
A.泊头老豆腐 B.羊肠子 C.连镇烧鸡 D.油酥烧饼
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“泊头老豆腐”的同学有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“富春包子”是扬州特色早点,富春茶社为了了解顾客对各种早点的喜爱情况,设计了如右图的调查问卷,对顾客进行了抽样调查.根据统计数据绘制了如下尚不完整的统计图.
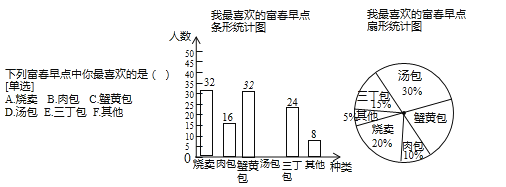
根据以上信息,解决下列问题:
(1)条形统计图中“汤包”的人数是 ,扇形统计图中“蟹黄包”部分的圆心角为 °;
(2)根据抽样调查结果,请你估计富春茶社1000名顾客中喜欢“汤包”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
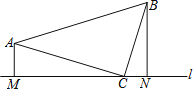
【题目】如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作直线![]() 的垂线,垂足分别为M、N.
的垂线,垂足分别为M、N.
(1)求证:△AMC≌△CNB;
(2)若AM=3,BN=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com