
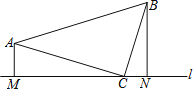
【题目】如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作直线![]() 的垂线,垂足分别为M、N.
的垂线,垂足分别为M、N.
(1)求证:△AMC≌△CNB;
(2)若AM=3,BN=5,求AB的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)由垂直定义得∠AMC =∠BNC=90°,再根据同角的余角相等得∠MAC=∠NCB,再由AAS证明△AMC≌△CNB.
(2)由△AMC≌△CNB得出CM=BN=5,再利用勾股定理就能计算BC,从而算出AB.
解:(1)∵AM⊥l,BN⊥l,∠ACB=90°,
∴∠AMC=∠ACB=∠BNC=90°,
∴∠MAC+∠MCA=90°,∠MCA+∠NCB=180﹣90°=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
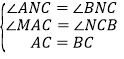
∴△AMC≌△CNB(AAS);
(2)由(1)知 △AMC≌△CNB,
∴CM=BN=5,
∴Rt△ACM中,AC=![]() ,
,
∵Rt△ABC,∠ACB=90°,AC=BC=![]() ,
,
∴AB=![]() =
=![]() =2
=2![]() .
.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,2016排列成如图所示的形式.

(1)用一个矩形随意框住4个数,把其中最小的数记为![]() ,另三个数用含
,另三个数用含![]() 式子表示出来,当被框住的4个数之和等于418时,
式子表示出来,当被框住的4个数之和等于418时,![]() 值是多少?
值是多少?
(2)被框住的4个数之和能否等于724?如果能,请求出此时x值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OD恰为∠BOE的平分线.
(1)图中∠BOC的补角是 把符合条件的角都填出来);
(2)若∠AOD=145°,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
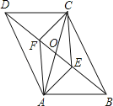
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com