Question

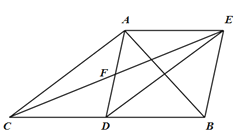
【题目】如图，在△ABC中，点D是BC的中点，点F是AD的中点，过点D作DE∥AC，交CF的延长线于点E，连接BE，AE．

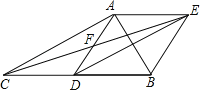
（1）求证：四边形ACDE是平行四边形；

（2）若AB=AC，试判断四边形ADBE的形状，并证明你的结论．

Answer 1

【答案】见试题解析

【解析】

试题分析：（1）首先证明△AFC≌△DFE，根据全等三角形对应边相等可得AC=DE，再根据一组对边平行且相等的四边形是平行四边形可得结论；

（2）首先证明四边形ADBE为平行四边形，再根据等腰三角形的性质可得AD⊥CB，进而可得四边形ADBE为矩形．

试题解析：（1）证明：∵DE∥AC，

∴∠CAF=∠EDF，

∵点F是AD的中点，

∴FA=DF，

在△AFC和△DFE中

∴△AFC≌△DFE（ASA），

∴AC=DE，

∴四边形ACDE是平行四边形；

（2）解：四边形ADBE为矩形，理由如下：

∵四边形ACDE是平行四边形，

∴AE=CD且AE∥CB，

∵点D是BC的中点，

∴CD=DB，

∴AE=BD且AE∥DB，

∴四边形ADBE为平行四边形，

又∵AB=AC，

∴AD⊥CB，

∴∠ADB=90°，

∴四边形ADBE为矩形．