
【题目】某校为开展体育大课间活动,需要购买篮球与足球若干个.已知购买2个篮球和3个足球共需要380元;购买4个篮球和5个足球共需要700元.
(1)求购买一个篮球、一个足球各需多少元;
(2)若体育老师带了8000元去购买这种篮球与足球共100个.由于数量较多,店主给出“一律打九折”的优惠价,那么他最多能购买多少个篮球?
【答案】(1)购买一个需要篮球100元,购买一个足球需要60元;(2)这所学校最多可以购买46个篮球.
【解析】
(1)设购买一个篮球需要x元,购买一个足球需要y元,列方程组,并解方程组可得;
(2) 设购买了a个篮球,则购买了(80﹣a)个足球.列不等式,并解不等式可得.
解:(1)设购买一个篮球需要x元,购买一个足球需要y元,列方程组得:
![]() ,
,
解得:![]() ,
,
答:购买一个需要篮球100元,购买一个足球需要60元.
(2)设购买了a个篮球,则购买了(80﹣a)个足球.列不等式得:
100×0.9a+60×0.9×(80﹣a)≤6000,
解得a≤46![]() .
.
∵a为正整数,
∴a最多可以购买46个篮球.
∴这所学校最多可以购买46个篮球.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】为了解学生课余活动情况,某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中书法部分的圆心角的度数;
(3)如果该校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的20名学生,估计每个兴趣小组至少需要准备多少名教师?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,∠ACB=90° AD 是它的角平分线,EB⊥AB 于点 B 且交 AD 的延长线于点 E.
(1)如图 1,求证:BD=BE
(2)如图 2,过点 E 作 EF⊥BC 于点 F, CF:BF=5:3, BE=10,求 DF 的长.
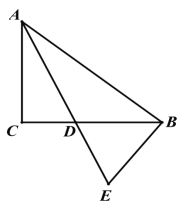
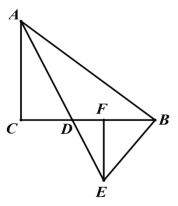
图 1 图 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点F是AD的中点,过点D作DE∥AC,交CF的延长线于点E,连接BE,AE.
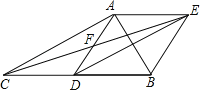
(1)求证:四边形ACDE是平行四边形;
(2)若AB=AC,试判断四边形ADBE的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课中,小辉将边长为![]() 和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
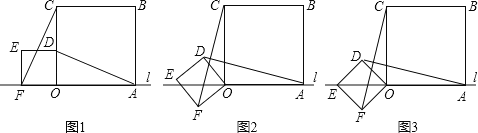
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
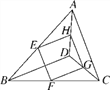
【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点,连接EF,FG,GH,HE.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“富春包子”是扬州特色早点,富春茶社为了了解顾客对各种早点的喜爱情况,设计了如右图的调查问卷,对顾客进行了抽样调查.根据统计数据绘制了如下尚不完整的统计图.
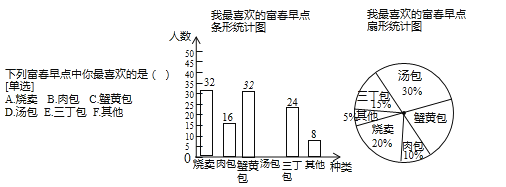
根据以上信息,解决下列问题:
(1)条形统计图中“汤包”的人数是 ,扇形统计图中“蟹黄包”部分的圆心角为 °;
(2)根据抽样调查结果,请你估计富春茶社1000名顾客中喜欢“汤包”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路,完成解答过程.
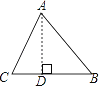
(1)作AD⊥BC于D,设BD=x,用含x的代数式表示CD,则CD=________;
(2)请根据勾股定理,利用AD作为“桥梁”建立方程,并求出x的值;
(3)利用勾股定理求出AD的长,再计算三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com