Question

【题目】在△ABC 中，∠ACB=90° AD 是它的角平分线，EB⊥AB 于点 B 且交 AD 的延长线于点 E.

（1）如图 1，求证：BD=BE

（2）如图 2，过点 E 作 EF⊥BC 于点 F, CF:BF=5:3, BE=10,求 DF 的长.

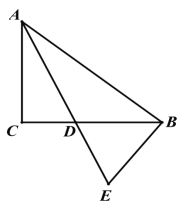
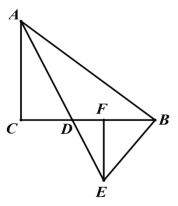
图 1 图 2

Answer 1

【答案】（1）证明见解析.（2）DF=4

【解析】分析: （1）过点B作BG⊥DE于G, 根据AD是△ABC的角平分线, EB⊥AB得∠ADC=∠E, 再证∠BGD=∠BGE,最后根据BG=BG可证△BDG≌△BEG,从而可得BD=BE.

（2）过点D作DH⊥AB于H，先证△BHD≌△EBF,得到 DH=BF,从而CD=BF.设CF=5x,BF=3x,根据BD=BF+DF可求出x的值,可求出DF的值.

详解:

（1）证明：过点B作BG⊥DE于G

∵AD是△ABC的角平分线

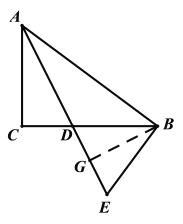
∴∠BAD=∠CAD

∵EB⊥AB

∴∠ABE=90°

在Rt△ABE中

∠BAE+∠E=90°

在Rt△ACD中

∠CAD+∠ADC=90°

∴∠ADC=∠E

∵∠ADC=∠BDE

∴∠BDE=∠E

∵BG⊥DE

∴∠BGD=∠BGE

∵BG=BG

∴△BDG≌△BEG（AAS）

∴BD=BE

（2）过点D作DH⊥AB于H，

∵ ∠ACB=90°

∴ CD⊥AC

∴ CD=DH

∵ ∠ABE=90°

∴ ∠ABC+∠FBE=90

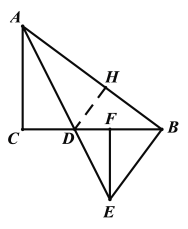
∵ EF⊥BD

∴ ∠BFE=90°

∴ ∠FEB+∠FBE=90°

∴ ∠HBD=∠FEB

∵ DH⊥AB

∴ ∠BHD=90°

∴ △BHD≌△EBF（AAS）

∴ DH=BF

∴ CD=BF

∵ CF:BF=5:3

∵ 设CF=5x,BF=3x,则CD=3x,

DF=CF-CD=5x-3x=2x

BD=BF+DF=3x+2x==5x

∵ BE=10

∴ 5x=10,x=2

∴ DF=2×2=4