练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在笔直的铁路上A、B两点相距25km，C、D为两村庄，DA=10km，CB=15km，DA⊥AB于A，CB⊥AB于B，现要在AB上建一个中转站E，使得C、D两村到E站的距离相等．求E应建在距A多远处？

    【答案】E应建在距A点15km处

    【解析】试题分析：设AE=x，则BE=25-x，=根据勾股定理可得DE2=AD2+AE2=102+x2，CE2=BC2+BE2=152+（25-x）2，由DE=CE可得102+x2=152+（25-x）2，再解方程即可.

    试题解析：设AE=x，则BE=25-x，

    在Rt△ADE中，

    DE2=AD2+AE2=102+x2，

    在Rt△BCE中，

    CE2=BC2+BE2=152+（25-x）2，

    由题意可知：DE=CE，

    所以：102+x2=152+（25-x）2，

    解得：x=15．

    所以E应建在距A点15km处.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC，直线PQ垂直平分AC，与边AB交于E，连接CE，过点C作CF平行于BA交PQ于点F，连接AF．

    （1）求证：△AED≌△CFD；

    （2）求证：四边形AECF是菱形．

    （3）若AD=3，AE=5，则菱形AECF的面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD是∠BAC的平分线，AD的垂线平分线交AB于点F，交BC的延长线于点E，连接AE，DF.

    求证：（1）∠EAD=∠EDA；（2）DF//AC；（3）∠EAC=∠B.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC 中，∠ACB=90° AD 是它的角平分线，EB⊥AB 于点 B 且交 AD 的延长线于点 E.

    （1）如图 1，求证：BD=BE

    （2）如图 2，过点 E 作 EF⊥BC 于点 F, CF:BF=5:3, BE=10,求 DF 的长.

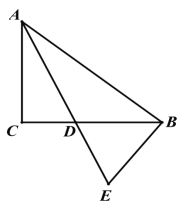
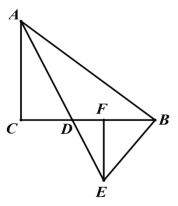
    图 1 图 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，

    ∠BAD＝45°，AD与BE交于点F，连接CF.

    （1）求证：BF＝2AE；

    （2）若CD＝，求AD的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D是BC的中点，点F是AD的中点，过点D作DE∥AC，交CF的延长线于点E，连接BE，AE．

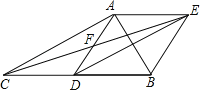
    （1）求证：四边形ACDE是平行四边形；

    （2）若AB=AC，试判断四边形ADBE的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在数学活动课中，小辉将边长为和3的两个正方形放置在直线l上，如图1，他连结AD、CF，经测量发现AD=CF．

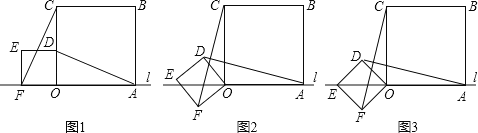
    （1）他将正方形ODEF绕O点逆时针旋转一定的角度，如图2，试判断AD与CF还相等吗？说明你的理由；

    （2）他将正方形ODEF绕O点逆时针旋转，使点E旋转至直线l上，如图3，请你求出CF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

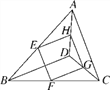
    【题目】如图，E，F，G，H分别是边AB，BC，CD，DA的中点，连接EF，FG，GH，HE.

    (1)判断四边形EFGH的形状，并证明你的结论；

    (2)当BD，AC满足什么条件时，四边形EFGH是正方形？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

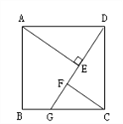
    【题目】四边形ABCD是正方形，G是BC上任意一点（点G与B、C不重合），AE⊥DG于E，CF∥AE交DG于F.

    （1） 在图中找出一对全等三角形，并加以证明；

    （2）求证：AE=FC+EF.

    查看答案和解析>>

    同步练习册答案