
����Ŀ����ͼ������ABC�У�AB=15��BC=14��AC=13������ABC������� ijѧϰС�龭����������������������Ľ���˼·�����㰴�����ǵĽ���˼·����ɽ����̣�
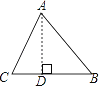
(1)��AD��BC��D����BD=x���ú�x�Ĵ���ʽ��ʾCD����CD=________��
(2)����ݹ��ɶ���������AD��Ϊ���������������̣������x��ֵ��
(3)���ù��ɶ������AD�ij����ټ��������ε������
���𰸡���1��14��x;(2)9����3��84
�������������������1����֪BC=14����BD=x����CD=BC-BD=14-x����2���� Rt��ABD �У����ݹ��ɶ������AD���� Rt��ACD �У����ݹ��ɶ������AD�����������г����̣��ⷽ�̼��ɣ���3���ڣ�2���Ļ��������AD�ij��������������ε������ʽ��⼴��.
���������
��1��CD=(14-x)
��2���� AD �� BC ���ϵĸߣ�
���ABD ����ACD ����ֱ�������Σ�
�� Rt��ABD �У����ݹ��ɶ�����AD=AB-BD=15-x
�� Rt��ACD �У����ݹ��ɶ�������AD=AC-CD=13-��14-x��
��15-x=13-��14-x��
��ã�x=9����BD=9.
��3��AD=15-9=225-81=144����AD=12
����![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��չ������μ�����Ҫ�����������������ɸ�����֪����2�������3��������Ҫ380Ԫ������4�������5��������Ҫ700Ԫ��
(1)����һ������һ������������Ԫ��
(2)��������ʦ����8000Ԫȥ������������������100�������������϶࣬����������һ�ɴ���ۡ����Żݼۣ���ô������ܹ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
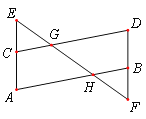
����Ŀ����֪����ͼ����A����D����EGC����FHB
��1����֤��AB��CD
��2����֤����E����F
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC������OΪAC���ϵ�һ������������O��ֱ��MN��BC����MN����BCA�����ƽ����CF�ڵ�F������ACB�ڽ�ƽ����CE��E��

��1����֤��EO=FO��
��2������O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���֤����Ľ��ۣ�
��3����AC���ϴ��ڵ�O��ʹ�ı���AECF����������������ABC����״��֤����Ľ��ۡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������( )
A. ���![]() ����
���� ![]()
B. ���|a|=|b|����ôa=b
C. ������ǵĺ��Ƕ۽�
D. ���һ�㵽�߶����˵ľ�����ȣ���ô����������߶ε��е�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
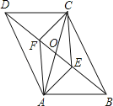
����Ŀ����ͼ���ı���ABCD�У�AB=CD���Խ���AC��BD�ཻ�ڵ�O��AE��BD�ڵ�E��CF��BD�ڵ�F������AF��CE����DE=BF�������н��ۣ���CF=AE����OE=OF�����ı���ABCD��ƽ���ı��Σ���ͼ�й����Ķ�ȫ�������Σ�������ȷ���۵ĸ����ǣ�������
A��4 B��3 C��2 D��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ѵ���ָ���Բ��ת��A��B�ֱ�ֳ�4�ȷݡ�3�ȷݵ�����������ÿһ��С�����ڱ������֣���ͼ��ʾ����С����С����������ת����Ϸ����Ϸ�����ǣ�ͬʱת������ת�̣���ת��ֹͣʱ����ָ����ָ�����������֮��Ϊ3�ı�������С��ʤ������С��ʤ��������ָ�����ڷָ����ϣ�����Ч��������ת��ת�̣� 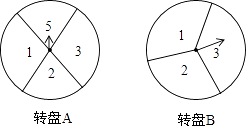
��1�������б�����״ͼ�ķ�������С����ʤ�ĸ��ʣ�
��2�����������Ϸ�����С����С��˫����ƽ�������жϲ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���ABC+��D=180����ACƽ�֡�BAD��CE��AB��CF��AD����˵����
��1����CBE�ա�CDF��
��2��AB+DF=AF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y=x2+bx+c��A��B��C���㣬��A�������ǣ�3��0������C�������ǣ�0����3��������P���������ϣ�
��1��b= �� c= �� ��B������Ϊ����ֱ����д�����
��2���Ƿ���ڵ�P��ʹ�á�ACP����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
��3��������P��PE��ֱy���ڵ�E����ֱ��AC�ڵ�D������D��x��Ĵ��ߣ�����ΪF������EF�����߶�EF�ij������ʱ�������P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com