【题目】如图，四边形ABCD中，∠ABC+∠D=180°，AC平分∠BAD，CE⊥AB，CF⊥AD．试说明：
（1）△CBE≌△CDF；
（2）AB+DF=AF．
【答案】（1）证明见解析；（2）证明见解析.
【解析】试题分析：（1）根据角平分线的性质可得到CE=CF，根据余角的性质可得到∠EBC=∠D，已知CE⊥AB，CF⊥AD，从而利用AAS即可判定△CBE≌△CDF．
（2）已知EC=CF，AC=AC，则根据HL判定△ACE≌△ACF得AE=AF，最后证得AB+DF=AF即可．
试题解析：证明：（1）∵AC平分∠BAD，CE⊥AB，CF⊥AD
∴CE=CF
∵∠ABC+∠D=180°，∠ABC+∠EBC=180°
∴∠EBC=∠D
在△CBE与△CDF中，
,
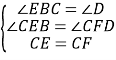∴△CBE≌△CDF；
（2）在Rt△ACE与Rt△ACF中，
∴△ACE≌△ACF
∴AE=AF
∴AB+DF=AB+BE=AE=AF．
七星图书口算速算天天练系列答案科目：初中数学 来源： 题型：
【题目】“富春包子”是扬州特色早点，富春茶社为了了解顾客对各种早点的喜爱情况，设计了如右图的调查问卷，对顾客进行了抽样调查．根据统计数据绘制了如下尚不完整的统计图．
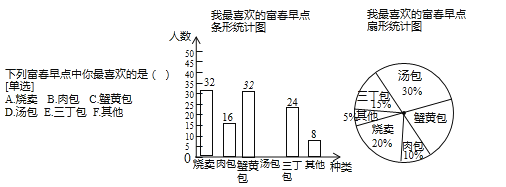
根据以上信息，解决下列问题：
（1）条形统计图中“汤包”的人数是 ，扇形统计图中“蟹黄包”部分的圆心角为 °；
（2）根据抽样调查结果，请你估计富春茶社1000名顾客中喜欢“汤包”的有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积． 某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路，完成解答过程．
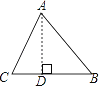
(1)作AD⊥BC于D，设BD=x，用含x的代数式表示CD，则CD=________；
(2)请根据勾股定理，利用AD作为“桥梁”建立方程，并求出x的值；
(3)利用勾股定理求出AD的长，再计算三角形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小颖和小红两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）试验，她们共做了60次试验，试验的结果如下：
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
（1）计算“3点朝上”的频率和“5点朝上”的频率.
（2）小颖说：“根据上述试验，一次试验中出现5点朝上的概率最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
（1）在图1中以格点为顶点画一个面积为5的等腰直角三角形；
（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、
、 
；
（3）如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于三个数a，b，c，用M{a，b，c}表示这三个数的平均数，用min{a，b，c}表示这三个数中最小的数．例如：M{－1，2，3}＝
，min{－1，2，3}＝－1，如果M{3，2x＋1，4x－1}＝min{2，－x＋3，5x}，那么x＝____________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点A坐标为(6，0)，点B在y轴的正半轴上，且
=240.
(1)求点B坐标；
(2)若点P从B出发沿y轴负半轴方向运动，速度每秒2个单位，运动时间t秒，△AOP的面积为S，求S与t的关系式，并直接写出t的取值范围；
(3)在(2)的条件下，若S△AOP：S△ABP=1:3，且S△AOP+S△ABP=S△AOB，在线段AB的垂直平分线上是否存在点Q，使得△AOQ的面积与△BPQ的面积相等？若存在，求出Q点坐标；若不存在，请说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知等腰Rt△ABC中，∠BAC=90°．点D从点B出发沿射线BC移动，以AD为腰作等腰Rt△ADE，∠DAE=90°．连接CE．
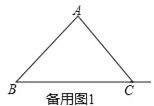
（1）如图，求证：△ACE≌△ABD；
（2）点D运动时，∠BCE的度数是否发生变化？若不变化，求它的度数；若变化，说明理由；
（3）若AC=
，当CD=1时，请求出DE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
