
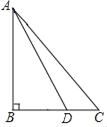
【题目】在△ABC中,∠B=90°,AB=BC,点D是BC边上的一点,连接AD,将AD绕点D顺时针旋转90°得到DE,作EF⊥BC交BC的延长线于点F.
(1)依题意补全图形;
(2)求证:EF=CF.
【答案】(1)如图所示见解析;(2)见解析.
【解析】
(1)依据AD绕点D顺时针旋转90°得到DE,作EF⊥BC交BC的延长线于点F进行作图.
(2)依据AAS判定△ABD≌△DFE,即可得到BD=EF,AB=DF,再根据AB=BC,可得BC=DF,进而得出BD=CF,等量代换可得EF=CF.
(1)如图所示:

(2)证明:由题可得,∠ADE=∠B=90°,AD=ED,
∴∠BAD+∠ADB=∠ADB+∠EDF=90°,
∴∠BAD=∠EDF,
在△ABD和△DFE中,
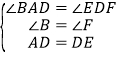 ,
,
∴△ABD≌△DFE(AAS),
∴BD=EF,AB=DF,
又∵AB=BC,
∴BC=DF,
∴BC﹣CD=DF﹣CD,即BD=CF,
∴EF=CF.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程(k﹣2)2x2+(2k+1)x+1=0有实数解,且反比例函数y=![]() 的图象经过第二、四象限,若k是常数,则k的值为( )
的图象经过第二、四象限,若k是常数,则k的值为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m,拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
(1)如图1,若BC=4m,则S=_____m2.
(2)如图2,现考虑在(1)中矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其他条件不变,则在BC的变化过程中,当S取得最小值时,边BC的长为____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
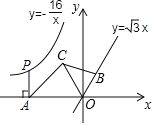
【题目】如图,点P是反比例函数![]() 图象上的一动点,
图象上的一动点,![]() 轴于点A,在直线
轴于点A,在直线![]() 上截取
上截取![]() 点B在第一象限
点B在第一象限![]() ,点C的坐标为
,点C的坐标为![]() ,连接AC、BC、OC.
,连接AC、BC、OC.
![]() 填空:
填空:![]() ______,
______,![]() ______;
______;
![]() 求证:
求证:![]() ∽
∽![]() ;
;
![]() 随着点P的运动,
随着点P的运动,![]() 的大小是否会发生变化?若变化,请说明理由,若不变,则求出它的大小.
的大小是否会发生变化?若变化,请说明理由,若不变,则求出它的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )

A. sinα=cosα B. tanC=2 C. sinβ=![]() D. tanα=1
D. tanα=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() x﹣2与x轴交于点A,与y轴交于点C,抛物线y=
x﹣2与x轴交于点A,与y轴交于点C,抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC下方抛物线上一点,且∠ACD=2∠BAC,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形ABC中,∠ACB=900,AB=10, BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F.现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1.若△E1FA1∽△E1BF,则AD= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com