练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】△ABC在网格中的位置如图所示（每个小正方形边长为1），AD⊥BC于D，下列选项中，错误的是（　　）

    A. sinα＝cosα B. tanC＝2 C. sinβ＝ D. tanα＝1

    【答案】C

    【解析】

    试题由图可分别求得BD=AD=2，AB=2，CD=1，AC=，利用锐角三角函数定义在Rt△ABD和Rt△ACD中计算即可判断．

    解：由图可得BD=AD=2，CD=1，

    所以AB==2，AC==，

    在Rt△ABD中，sinα==，cosα==，tanα==1,

    在Rt△ACD中，sinβ==，cosβ==，tanC==2,

    则sinα＝cosα，故A正确；tanC＝2，故B正确；sinβ≠cosβ，故C错误；tanα=1，故D正确.

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

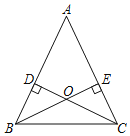
    【题目】如图，锐角三角形ABC的两条高线BE、CD相交于点O，BE＝CD．

    （1）求证：BD＝CE；

    （2）判断点O是否在∠BAC的平分线上，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（12分）如图所示是隧道的截面由抛物线和长方形构成，长方形的长是12 m，宽是4 m．按照图中所示的直角坐标系，抛物线可以用y=x2+bx+c表示，且抛物线上的点C到OB的水平距离为3 m，到地面OA的距离为m.

    （1）求抛物线的函数关系式，并计算出拱顶D到地面OA的距离；

    （2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向车道，那么这辆货车能否安全通过？

    （3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，以AB为腰向正方形内部作等腰△ABE，点G在CD上，且CG=3DG．连接BG并延长，与AE交于点F，与AD延长线交于点H．连接DE交BH于点K，连接CK．若AE2=BFBH，FG=，则S四边形EFKC=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，E为AB边的中点，以BE为边作等边△BDE，连接AD，CD．

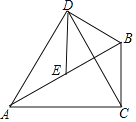
    （1）求证：△ADE≌△CDB；

    （2）若BC＝1，在AC边上找一点H，使得BH+EH最小，并求出这个最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ACB中，∠ACB=90°，∠A=60°，CD、CE分别是△ABC的高和中线，下列说法错误的是( )

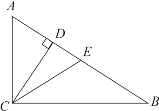
    A.AD =ABB.S△CEB = S△ACE

    C.AC、BC的垂直平分线都经过ED.图中只有一个等腰三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，某村要设计修建一条引水渠，渠道的横断面为等腰梯形，渠道底面宽0.8m，渠道内坡度是1：0.5．引水时，水面要低于渠道上沿0.2m，水流的横断面（梯形ABFE）的面积为1.3m2，求水渠的深度h．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，BC=2，AC=2，点D是BC的中点，点E是边AB上一动点，沿DE所在直线把△BDE翻折到△B′DE的位置，B′D交AB于点F．若△AB′F为直角三角形，则AE的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知如图，是腰长为的等腰直角三角形，要求在其内部作出一个半圆，直径在的边上，且半圆的弧与的其他两边相切，则该半圆的半径是________（结果保留根号）．

    查看答案和解析>>

    同步练习册答案