
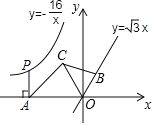
【题目】如图,点P是反比例函数![]() 图象上的一动点,
图象上的一动点,![]() 轴于点A,在直线
轴于点A,在直线![]() 上截取
上截取![]() 点B在第一象限
点B在第一象限![]() ,点C的坐标为
,点C的坐标为![]() ,连接AC、BC、OC.
,连接AC、BC、OC.
![]() 填空:
填空:![]() ______,
______,![]() ______;
______;
![]() 求证:
求证:![]() ∽
∽![]() ;
;
![]() 随着点P的运动,
随着点P的运动,![]() 的大小是否会发生变化?若变化,请说明理由,若不变,则求出它的大小.
的大小是否会发生变化?若变化,请说明理由,若不变,则求出它的大小.
【答案】(1)4;![]() (2)证明见解析(3)120°
(2)证明见解析(3)120°
【解析】
(1)过点C作CE⊥x轴于点E,过点B作BF⊥x轴于点F,由点C的坐标可得出OE,CE的长度,进而可求出OC的长度及∠AOC的度数,由直线OB的解析式可得出∠BOF的度数,再利用∠BOC=180°﹣∠AOC﹣∠BOF即可求出∠BOC的度数;
(2)由(1)可知∠AOC=∠BOC,由点P是反比例函数y![]() (x<0)图象上的一动点,利用反比例函数图象上点的坐标特征可得出PAOA=16,结合OB=PA及OC=4,可得出
(x<0)图象上的一动点,利用反比例函数图象上点的坐标特征可得出PAOA=16,结合OB=PA及OC=4,可得出![]() ,结合∠AOC=∠BOC即可证出△AOC∽△COB;
,结合∠AOC=∠BOC即可证出△AOC∽△COB;
(3)由△AOC∽△COB利用相似三角形的性质可得出∠CAO=∠BCO.在△AOC中,利用三角形内角和定理可求出∠CAO+∠OCA=120°,进而可得出∠BCO+∠OCA=120°,即∠ACB=120°.
(1)过点C作CE⊥x轴于点E,过点B作BF⊥x轴于点F,如图所示.
∵点C的坐标为(﹣2,2![]() ),∴OE=2,CE=2
),∴OE=2,CE=2![]() ,∴OC
,∴OC![]() 4.
4.
∵tan∠AOC![]() ,∴∠AOC=60°.
,∴∠AOC=60°.
∵直线OB的解析式为y![]() x,∴∠BOF=60°,∴∠BOC=180°﹣∠AOC﹣∠BOF=60°.
x,∴∠BOF=60°,∴∠BOC=180°﹣∠AOC﹣∠BOF=60°.
故答案为:4;60°.
(2)∵∠AOC=60°,∠BOC=60°,∴∠AOC=∠BOC.
∵点P是反比例函数y![]() (x<0)图象上的一动点,∴PAOA=16.
(x<0)图象上的一动点,∴PAOA=16.
∵PA=OB,∴OBOA=16=OC2,即![]() ,∴△AOC∽△COB.
,∴△AOC∽△COB.
(3)∠ACB=120°,不会发生变化.理由如下:
∵△AOC∽△COB,∴∠CAO=∠BCO.
在△AOC中,∠AOC=60°,∴∠CAO+∠OCA=120°,∴∠BCO+∠OCA=120°,即∠ACB=120°.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD平分∠ABC,DE⊥AB,AE=6,cos A=![]() .求:
.求:
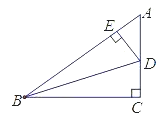
(1)DE,CD的长;(2)tan∠DBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
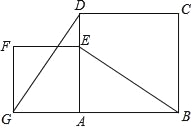
【题目】将边长为2![]() 的正方形ABCD与边长为2的正方形AEFG如图放置,AD与AE在同一直线上,AB与AG在同一直线上,连接DG、BE.
的正方形ABCD与边长为2的正方形AEFG如图放置,AD与AE在同一直线上,AB与AG在同一直线上,连接DG、BE.
(1)求证:DG=BE;
(2)把正方形AEFG绕点A旋转,当点F恰好落在AB边所在的直线上时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若![]() .
.
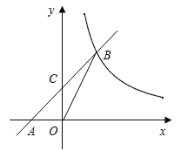
(1)求该反比例函数的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
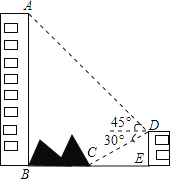
【题目】如图,大楼底右侧有一障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为![]() ,测得大楼顶端A的仰角为
,测得大楼顶端A的仰角为![]() 点B,C,E在同一水平直线上
点B,C,E在同一水平直线上![]() 已知
已知![]() ,
,![]() ,则障碍物B,C两点间的距离为______
,则障碍物B,C两点间的距离为______![]() 结果保留根号
结果保留根号![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
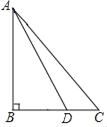
【题目】在△ABC中,∠B=90°,AB=BC,点D是BC边上的一点,连接AD,将AD绕点D顺时针旋转90°得到DE,作EF⊥BC交BC的延长线于点F.
(1)依题意补全图形;
(2)求证:EF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3b+4c>0;④4a﹣2b≥at2+bt(t为实数);⑤点(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(﹣
,y2),(﹣![]() ,y3)是该抛物线上的点,则y1<y2<y3,其中正确的结论有( )
,y3)是该抛物线上的点,则y1<y2<y3,其中正确的结论有( )

A. ②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瓦子街是上杭城关老城区改造的商业文化购物步行街,瓦子街某商场经营的某个品牌童装,购进时的单价是60元,根据市场调查,在一段时间内,销售单价是80元时,销售量是200件,销售单价每降低1元,就可多售出20件.
![]() 求出销售量
求出销售量![]() 件
件![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售该品牌童装获得的利润
求出销售该品牌童装获得的利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 若童装厂规定该品牌童装的销售单价不低于76元且不高于80元,则商场销售该品牌童装获得的最大利润是多少?
若童装厂规定该品牌童装的销售单价不低于76元且不高于80元,则商场销售该品牌童装获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com