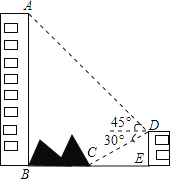
【题目】如图，大楼底右侧有一障碍物，在障碍物的旁边有一栋小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为
，测得大楼顶端A的仰角为
点B，C，E在同一水平直线上
已知
，
，则障碍物B，C两点间的距离为______
结果保留根号
黄冈天天练口算题卡系列答案科目：初中数学 来源： 题型：
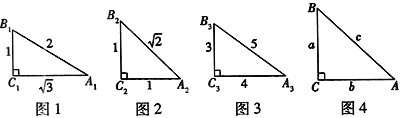
【题目】如图1，2，3，根据图中数据完成填空，再按要求答题：sin2A1＋sin2B1=____；sin2A2＋sin2B2=____；sin2A3＋sin2B3=____.
(1)观察上述等式，猜想：在Rt△ABC中，∠C=90°，都有sin2A＋sin2B=____；
(2)如图4，在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边分别是a，b，c，利用三角函数的定义和勾股定理证明你的猜想；
(3)已知∠A＋∠B=90°，且sinA=
，求sinB的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
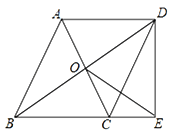
【题目】如图，□ABCD的对角线交于点O，点E在边BC的延长线上，且OE=OB，连接DE．
（1）求证：△BDE是直角三角形；
（2）如果OE⊥CD，试判断△BDE与△DCE是否相似，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知一次函数y=kx+b的图象与反比例函数
的图象交于A，B两点，且点A的横坐标和点B的纵坐标都是﹣2，
求：（1）一次函数的解析式；
（2）△AOB的面积；
（3）直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学为了提高学生的消防意识，举行了消防知识竞赛，所有参赛学生分别设有一、二、三等奖和纪念奖，获奖情况已绘制成如图所示的两幅不完整的统计图，根据图中所经信息解答下列问题：
（1）这次知识竞赛共有多少名学生？
（2）“二等奖”对应的扇形圆心角度数，并将条形统计图补充完整；
（3）小华参加了此次的知识竞赛，请你帮他求出获得“一等奖或二等奖”的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
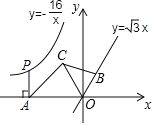
【题目】如图，点P是反比例函数
图象上的一动点，
轴于点A，在直线
上截取
点B在第一象限
，点C的坐标为
，连接AC、BC、OC．
填空：
______，
______；
求证：
∽
；
随着点P的运动，
的大小是否会发生变化？若变化，请说明理由，若不变，则求出它的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
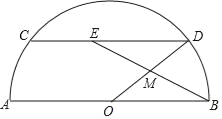
【题目】如图，半圆O的直径AB＝20，弦CD∥AB，动点M在半径OD上，射线BM与弦CD相交于点E（点E与点C、D不重合），设OM＝m．
（1）求DE的长（用含m的代数式表示）；
（2）令弦CD所对的圆心角为α，且sin
．
①若△DEM的面积为S，求S关于m的函数关系式，并求出m的取值范围；
②若动点N在CD上，且CN＝OM，射线BM与射线ON相交于点F，当∠OMF＝90° 时，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
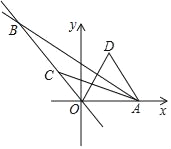
【题目】如图，在直角坐标系中，直线y＝﹣
x+
与x轴交于点A，与y＝﹣
x相交于点B，点C是线段OB上一动点，连接AC，在AC上方取点D，使得cos∠CAD＝
，且
＝
，连接OD，当点C从点O运动到点B时，线段OD扫过的面积为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰Rt△ABC中，BA=BC，∠ABC=90°，点D在AC上，将△ABD绕点B沿顺时针方向旋转90°后，得到△CBE．
（1）求∠DCE的度数；
（2）若AB=4，CD=3AD，求DE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
