
【题目】如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.

【答案】解:(1)90°;(2)2![]()
【解析】
试题(1)首先由等腰直角三角形的性质求得∠BAD、∠BCD的度数,然后由旋转的性质可求得∠BCE的度数,故此可求得∠DCE的度数;
(2)由(1)可知△DCE是直角三角形,先由勾股定理求得AC的长,然后依据比例关系可得到CE和DC的长,最后依据勾股定理求解即可.
试题解析:(1)∵△ABCD为等腰直角三角形,
∴∠BAD=∠BCD=45°.
由旋转的性质可知∠BAD=∠BCE=45°.
∴∠DCE=∠BCE+∠BCA=45°+45°=90°.
(2)∵BA=BC,∠ABC=90°,
∴AC=![]() .
.
∵CD=3AD,
∴AD=![]() ,DC=3
,DC=3![]() .
.
由旋转的性质可知:AD=EC=![]() .
.
∴DE=![]() .
.


科目:初中数学 来源: 题型:
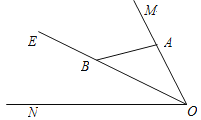
【题目】如图,已知∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.当AB⊥OM,且△ADB有两个相等的角时,∠OAC的度数为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
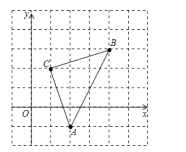
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
(1)写出点A、B的坐标:A(_____,_____)、B(_____,_____);
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,写出A′、B′、C′三点坐标;
(3)求△ABC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季来临,天气逐渐炎热起来.某商店将某种碳酸饮料每瓶的价格上调了10%,将某种果汁饮料每瓶的价格下调了5%,已知调价前买这两种饮料各一瓶共花费7元,调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费17.5元.
(1)若设调价前每瓶碳酸饮料![]() 元,每瓶果汁饮料
元,每瓶果汁饮料![]() 元,调价后每瓶碳酸饮料 元,每瓶果汁饮料 元(用含
元,调价后每瓶碳酸饮料 元,每瓶果汁饮料 元(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
(2)求这两种饮料在调价前每瓶各多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
A.![]()
B.2 ![]()
C.3
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1、用不超过16800元购进A、B两类图书共1000本; | |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
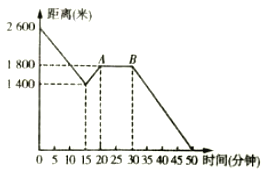
【题目】星期五小颖放学步行从学校回家,当她走了一段路后,想起要去买彩笔做画报,于是原路返回到刚经过的文具用品店,买到彩笔后继续往家走.如图是她离家的距离与所用时间的关系示意图,请根据图中提供的信息回答下列问题:
(1)小颖家与学校的距离是 米;
(2)![]() 表示的实际意义是 ;
表示的实际意义是 ;
(3)小颖本次从学校回家的整个过程中,走的路程是多少米?
(4)买到彩笔后,小颖从文具用品店回到家步行的速度是多少米/分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com