
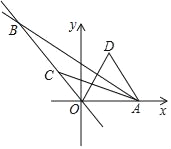
【题目】如图,在直角坐标系中,直线y=﹣![]() x+
x+![]() 与x轴交于点A,与y=﹣
与x轴交于点A,与y=﹣![]() x相交于点B,点C是线段OB上一动点,连接AC,在AC上方取点D,使得cos∠CAD=
x相交于点B,点C是线段OB上一动点,连接AC,在AC上方取点D,使得cos∠CAD=![]() ,且
,且![]() =
=![]() ,连接OD,当点C从点O运动到点B时,线段OD扫过的面积为_____.
,连接OD,当点C从点O运动到点B时,线段OD扫过的面积为_____.
【答案】![]() .
.
【解析】
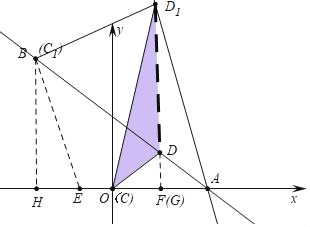
首先说明:当点C与B重合时,点D位于D1,此时AD1=![]() ,可知点D的运动轨迹是DD1,线段OD扫过的面积为△ODD1的面积;
,可知点D的运动轨迹是DD1,线段OD扫过的面积为△ODD1的面积;
解:∵直线y=﹣![]() x+
x+![]() 与x轴交于点A,
与x轴交于点A,
∴A(7,0),
由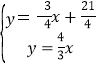 解得
解得![]() ,
,
∴B(﹣9,12),
作BH⊥x轴于H,则BH=12,OH=9,AH=16,
∴AB=![]() =20,
=20,
∴cos∠BAO=![]() ,
,
∵cos∠CAD=![]() ,
,
∴∠BAO=∠CAD,
当点C与O重合时,点D在线段AB上,
∵OA=7,OA:AD=7:5,
∴AD=5,作DF⊥OA于F,
∴DF=3,AF=4,OF=3,D(3,3),
当点C与B重合时,点D位于D1,此时AD1=![]() ,可知点D的运动轨迹是DD1,线段OD扫过的面积为△ODD1的面积,
,可知点D的运动轨迹是DD1,线段OD扫过的面积为△ODD1的面积,
在AH上取一点E,使得AE=BE,设AE=BE=x,
在Rt△BHE中,x2=122+(16﹣x)2,
∴x=![]() ,
,
∴BE=AE=![]() ,HE=
,HE=![]() ,作D1G⊥OA于G.
,作D1G⊥OA于G.
∵∠BAD1=∠BAO,∠BAO=∠EBA,
∴∠BEH=∠GAD1,
∴△BHE∽△D1GA,
∴![]() ,
,
∴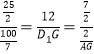 ,
,
∴D1F=![]() ,AG=4,
,AG=4,
∴OG=3(点F与G重合),
∴D1(3,![]() ),∵D(3,3),
),∵D(3,3),
∴DD1∥y,
∴![]() =
=![]() .
.
故答案是:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
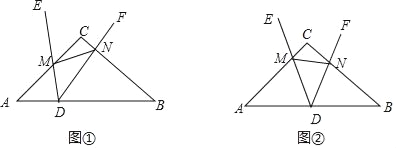
【题目】如图①,在△ABC中,AC=BC,点D是线段AB上一动点,∠EDF绕点D旋转,在旋转过程中始终保持∠A=∠EDF,射线DE与边AC交于点M,射线DE与边BC交于点N,连接MN.
(1)找出图中的一对相似三角形,并证明你的结论;
(2)如图②,在上述条件下,当点D运动到AB的中点时,求证:在∠EDF绕点D旋转过程中,点D到线段MN的距离为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
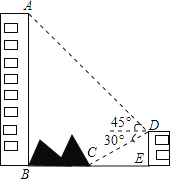
【题目】如图,大楼底右侧有一障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为![]() ,测得大楼顶端A的仰角为
,测得大楼顶端A的仰角为![]() 点B,C,E在同一水平直线上
点B,C,E在同一水平直线上![]() 已知
已知![]() ,
,![]() ,则障碍物B,C两点间的距离为______
,则障碍物B,C两点间的距离为______![]() 结果保留根号
结果保留根号![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3b+4c>0;④4a﹣2b≥at2+bt(t为实数);⑤点(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(﹣
,y2),(﹣![]() ,y3)是该抛物线上的点,则y1<y2<y3,其中正确的结论有( )
,y3)是该抛物线上的点,则y1<y2<y3,其中正确的结论有( )

A. ②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,BC=4,以BC的中点O为圆心分别与AB,AC相切于D、E两点,则![]() 的长为( )
的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瓦子街是上杭城关老城区改造的商业文化购物步行街,瓦子街某商场经营的某个品牌童装,购进时的单价是60元,根据市场调查,在一段时间内,销售单价是80元时,销售量是200件,销售单价每降低1元,就可多售出20件.
![]() 求出销售量
求出销售量![]() 件
件![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售该品牌童装获得的利润
求出销售该品牌童装获得的利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 若童装厂规定该品牌童装的销售单价不低于76元且不高于80元,则商场销售该品牌童装获得的最大利润是多少?
若童装厂规定该品牌童装的销售单价不低于76元且不高于80元,则商场销售该品牌童装获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
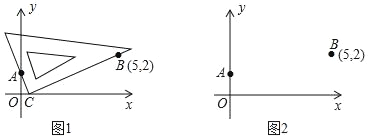
【题目】在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根,比如对于方程x2﹣5x+2=0,操作步骤是:第一步:根据方程系数特征,确定一对固定点A(0,1),B(5,2);第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C的横坐标m即为该方程的一个实数根(如图1);第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D的横坐标为n即为该方程的另一个实数根;(1)在图2中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹);(2)结合图1,请证明“第三步”操作得到的m就是方程x2﹣5x+2=0的一个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. 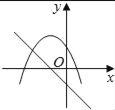 B.
B. 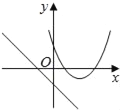 C.
C. 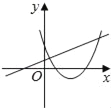 D.
D. 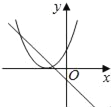
【答案】D
【解析】A.由函数y=mx+m的图象可知m<0,即函数y=mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,对称轴为x=![]() <0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<0,即函数y=mx2+2x+2开口方向朝上,对称轴为x=![]() <0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
故选:D.
【题型】单选题
【结束】
10
【题目】如图,已知菱形ABCD的周长为16,面积为![]() ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
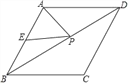
A. 2 B. 2![]() C. 4 D. 4
C. 4 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
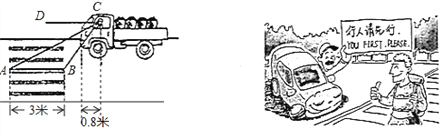
【题目】我国![]() 道路交通安全法
道路交通安全法![]() 第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”
第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行” ![]() 如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是
如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是![]() 和
和![]() ,如果斑马线的宽度是
,如果斑马线的宽度是![]() 米,驾驶员与车头的距离是
米,驾驶员与车头的距离是![]() 米,这时汽车车头与斑马线的距离x是多少?
米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com