
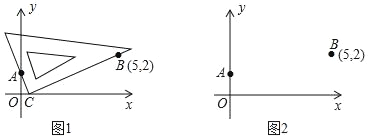
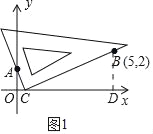
����Ŀ����ƽ��ֱ������ϵ�У�����ֱ�����ǰ�����ҵ�һԪ���η��̵�ʵ������������ڷ���x2��5x+2��0�����������ǣ���һ�������ݷ���ϵ��������ȷ��һ�Թ̶���A��0��1����B��5��2�����ڶ�����������ƽ�����ƶ�һ��ֱ�����ǰ壬ʹһ��ֱ�DZߺ����A����һ��ֱ�DZߺ����B�������������ƶ������У������ǰ��ֱ�Ƕ�������x���ϵ�C��ʱ����C�ĺ�����m��Ϊ�÷��̵�һ��ʵ��������ͼ1�������IJ����������ǰ�ֱ�Ƕ����λ�ã���������x������һ��D��ʱ����D�ĺ�����Ϊn��Ϊ�÷��̵���һ��ʵ��������1����ͼ2�У����ա����IJ����IJ�������������D���뱣��������Dʱֱ�����ǰ�����ֱ�DZߵĺۼ�������2�����ͼ1����֤�����������������õ���m���Ƿ���x2��5x+2��0��һ��ʵ������
���𰸡���1������������2����������
��������
��1��������������ͼ�μ��ɣ�
��2����ͼ1�У���BD��x����D���������������ε����ʼ��ɽ�����⣮
�⣺��1����D��ͼ��ʾ��
��2����ͼ1�У���BD��x����D��
�ߡ�AOC����ACB����CDB��90����
���ACO+��BCD��90������BCD+��CBD��90����
���ACO����CBD��
���ACO�ס�CBD��
��![]()
��![]()
�����ã�m2��5m+2��0��
��m�Ƿ���x2��5x+2��0��ʵ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
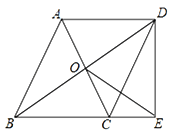
����Ŀ����ͼ����ABCD�ĶԽ��߽��ڵ�O����E�ڱ�BC���ӳ����ϣ���OE=OB������DE��
��1����֤����BDE��ֱ�������Σ�
��2�����OE��CD�����ж���BDE����DCE�Ƿ����ƣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
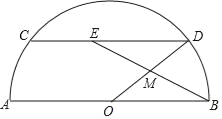
����Ŀ����ͼ����ԲO��ֱ��AB��20����CD��AB������M�ڰ뾶OD�ϣ�����BM����CD�ཻ�ڵ�E����E���C��D���غϣ�����OM��m��
��1����DE�ij����ú�m�Ĵ���ʽ��ʾ����
��2������CD���Ե�Բ�Ľ�Ϊ������sin![]() ��
��
������DEM�����ΪS����S����m�ĺ�����ϵʽ�������m��ȡֵ��Χ��
��������N��CD�ϣ���CN��OM������BM������ON�ཻ�ڵ�F������OMF��90�� ʱ����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
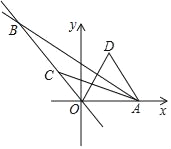
����Ŀ����ͼ����ֱ������ϵ�У�ֱ��y����![]() x+
x+![]() ��x�ύ�ڵ�A����y����
��x�ύ�ڵ�A����y����![]() x�ཻ�ڵ�B����C���߶�OB��һ���㣬����AC����AC�Ϸ�ȡ��D��ʹ��cos��CAD��
x�ཻ�ڵ�B����C���߶�OB��һ���㣬����AC����AC�Ϸ�ȡ��D��ʹ��cos��CAD��![]() ����
����![]() ��
��![]() ������OD������C�ӵ�O�˶�����Bʱ���߶�ODɨ�������Ϊ_____��
������OD������C�ӵ�O�˶�����Bʱ���߶�ODɨ�������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϲ��ش����⣺
����1�����һ�������ε����߳��ֱ�Ϊa��b��c����![]() ����ô�����ε����Ϊ
����ô�����ε����Ϊ![]() �� ��
�� ��
��ϣ������ѧ�Һ��ף�Heron��Լ��Ԫ50�꣩������ѧʷ���Խ�����β�����������������ڡ�������һ���У������˹�ʽ�ٺ�����֤������һ��ʽ�ƺ���ʽ��
�ҹ�������ѧ���ؾ��أ�Լ1202����Լ1261������������������ε�������������ؾ��ع�ʽ��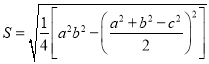 �� ��
�� ��
�������ǶԹ�ʽ�ڽ��б��Σ�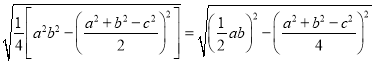

![]()
![]()
![]()
![]() ��
��
��˵������ʽ���ؾ��ع�ʽʵ������ͬһ��ʽ����������Ҳ�Ƣ�Ϊ���ש����ؾ��ع�ʽ��
���⣺��ͼ���ڡ�ABC�У�AB=13��BC=12��AC=7����O�����ڡ�ABC���е�ֱ���D��E��F��

��1�����ABC�������
��2�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB��4cm����E��Fͬʱ��C���������1cm/s���ٶȷֱ���CB��BA��CD��DA�˶�������Aʱֹͣ�˶������˶�ʱ��Ϊt(s)����AEF�����ΪS(cm2)����S(cm2)��t(s)�ĺ�����ϵ����ͼ���ʾΪ( )
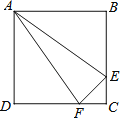
A. 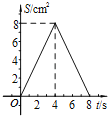 B.
B. 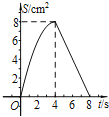
C. 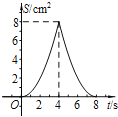 D.
D. 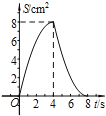
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������У�Ļ�У�ij��ȤС���������ͼ��ʾ��ֱ��ǽ��(�����㹻��)����32m�������Χ��һ�����λ�ABCD(���ֻΧAB��BC����)����AB��xm��
(1)���������Ϊ252m2����x��ֵ��
(2)����P����һ������ǽCD��AD�ľ���ֱ���17m��6m��Ҫ�������Χ�ڻ���(���߽磬���������Ĵ�ϸ)�������S�����ֵ��
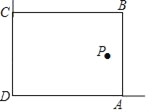
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Rt��ABC�У�BA=BC����ABC=90�㣬��D��AC�ϣ�����ABD�Ƶ�B��˳ʱ�뷽����ת90��õ���CBE��
��1�����DCE�Ķ�����
��2����AB=4��CD=3AD����DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD����O��ֱ����DF��BE���ң���DF��BE����֤����D����B��
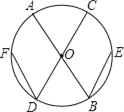
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com