
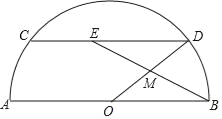
【题目】如图,半圆O的直径AB=20,弦CD∥AB,动点M在半径OD上,射线BM与弦CD相交于点E(点E与点C、D不重合),设OM=m.
(1)求DE的长(用含m的代数式表示);
(2)令弦CD所对的圆心角为α,且sin![]() .
.
①若△DEM的面积为S,求S关于m的函数关系式,并求出m的取值范围;
②若动点N在CD上,且CN=OM,射线BM与射线ON相交于点F,当∠OMF=90° 时,求DE的长.
【答案】(1)DE=![]() ;(2)①S=
;(2)①S=![]() ,(
,(![]() <m<10),②DE=
<m<10),②DE=![]() .
.
【解析】
(1)由CD∥AB知△DEM∽△OBM,可得![]() ,据此可得;
,据此可得;
(2)①连接OC、作OP⊥CD、MQ⊥CD,由OC=OD、OP⊥CD知∠DOP=![]() ∠COD,据此可得sin∠DOP=sin∠DMQ=
∠COD,据此可得sin∠DOP=sin∠DMQ=![]() 、sin∠ODP=
、sin∠ODP=![]() ,继而由OM=m、OD=10得QM=DMsin∠ODP=
,继而由OM=m、OD=10得QM=DMsin∠ODP=![]() (10﹣m),根据三角形的面积公式即可得;如图2,先求得PD=8、CD=16,证△CDM∽△BOM得
(10﹣m),根据三角形的面积公式即可得;如图2,先求得PD=8、CD=16,证△CDM∽△BOM得![]() ,求得OM=
,求得OM=![]() ,据此可得m的取值范围;
,据此可得m的取值范围;
②如图3,由BM=OBsin∠BOM=10×![]() =6,可得OM=8,根据(1)所求结果可得答案.
=6,可得OM=8,根据(1)所求结果可得答案.
(1)∵CD∥AB,
∴△DEM∽△OBM,
∴![]() ,即
,即![]() ,
,
∴DE=![]() ;
;
(2)①如图1,连接OC、作OP⊥CD于点P,作MQ⊥CD于点Q,
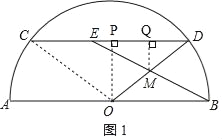
∵OC=OD、OP⊥CD,
∴∠DOP=![]() ∠COD,
∠COD,
∵sin![]() =
=![]() ,
,
∴sin∠DOP=sin∠DMQ=![]() ,sin∠ODP=
,sin∠ODP=![]() ,
,
∵OM=m、OD=10,
∴DM=10﹣m,
∴QM=DMsin∠ODP=![]() (10﹣m),
(10﹣m),
则S△DEM=![]() DEMQ=
DEMQ=![]() ×
×![]() ×
×![]() (10﹣m)=
(10﹣m)=![]() ,
,
如图2,
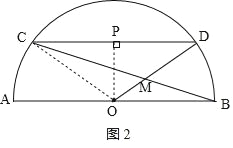
∵PD=ODsin∠DOP=10×![]() =8,
=8,
∴CD=16,
∵CD∥AB,
∴△CDM∽△BOM,
∴![]() ,即
,即![]() ,
,
解得:OM=![]() ,
,
∴![]() <m<10,
<m<10,
∴S=![]() ,(
,(![]() <m<10).
<m<10).
②当∠OMF=90°时,如图3,
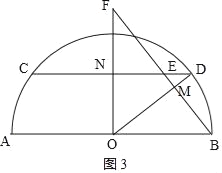
则∠BMO=90°,
在Rt△BOM中,BM=OBsin∠BOM=10×![]() =6,
=6,
则OM=8,
由(1)得DE=![]() .
.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的解析式;
(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;
(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
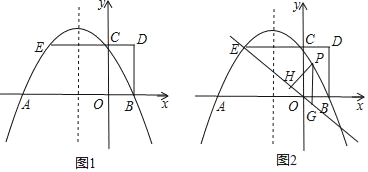
查看答案和解析>>
科目:初中数学 来源: 题型:
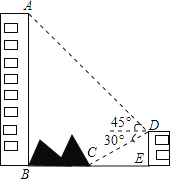
【题目】如图,大楼底右侧有一障碍物,在障碍物的旁边有一栋小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为![]() ,测得大楼顶端A的仰角为
,测得大楼顶端A的仰角为![]() 点B,C,E在同一水平直线上
点B,C,E在同一水平直线上![]() 已知
已知![]() ,
,![]() ,则障碍物B,C两点间的距离为______
,则障碍物B,C两点间的距离为______![]() 结果保留根号
结果保留根号![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3b+4c>0;④4a﹣2b≥at2+bt(t为实数);⑤点(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(﹣
,y2),(﹣![]() ,y3)是该抛物线上的点,则y1<y2<y3,其中正确的结论有( )
,y3)是该抛物线上的点,则y1<y2<y3,其中正确的结论有( )

A. ②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,BC=4,以BC的中点O为圆心分别与AB,AC相切于D、E两点,则![]() 的长为( )
的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
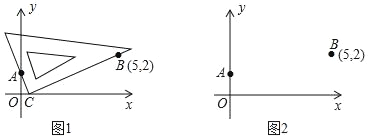
【题目】在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根,比如对于方程x2﹣5x+2=0,操作步骤是:第一步:根据方程系数特征,确定一对固定点A(0,1),B(5,2);第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C的横坐标m即为该方程的一个实数根(如图1);第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D的横坐标为n即为该方程的另一个实数根;(1)在图2中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹);(2)结合图1,请证明“第三步”操作得到的m就是方程x2﹣5x+2=0的一个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
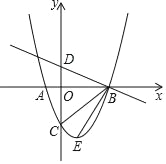
【题目】如图,抛物线y=ax2+bx﹣3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交子点C,且OB=OC=3OA,直线y=﹣![]() x+1与y轴交于点D.求∠DBC﹣∠CBE=_____.
x+1与y轴交于点D.求∠DBC﹣∠CBE=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com