练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

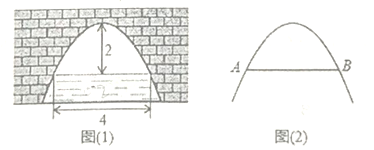
    【题目】如图（1）是一个横断面为抛物线形状的拱桥，当水面宽为时，拱顶与水面距离为.

    （1）请你在图（2）中，建立适当的平面直角坐标系，使该抛物线拱桥的函数关系式符合形式，并求此时，函数关系式；

    （2）当水面上升时，求水面宽度.

    【答案】（1）；（2）.

    【解析】

    （1）以抛物线的顶点为坐标原点，线段的中垂线为轴建立坐标系，再利用待定系数法求得函数解析式；

    （2）求出（1）中所求函数解析式时的值，据此可得.

    （1）建立平面直角坐标系，则通过画图可得知为原点，

    抛物线以轴为对称轴，且经过、两点，抛物线顶点坐标为，

    通过以上条件可设顶点式，其中可通过代入点坐标，

    到抛物线解析式得出：，

    所以抛物线解析式为；

    （2）水面上升m，

    ，

    故，

    解得：，，

    则水面的宽为（）.

    答：水面宽度为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

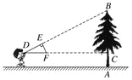
    【题目】如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上，已知纸板的两条直角边DE＝50 cm，EF＝25 cm，测得边DF离地面的高度AC＝1.6 m，CD＝10 m，则树高AB等于(　　)

    A. 4 m

    B. 5 m

    C. 6.6 m

    D. 7.7 m

    查看答案和解析>>

    科目：初中数学 来源： 题型：

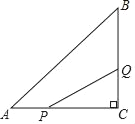
    【题目】如图，在△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，点P从点A沿AC向C以2cm/s的速度移动，到C即停，点Q从点C沿CB向B以1cm/s的速度移动，到B就停．

    （1）若P、Q同时出发，经过几秒钟S△PCQ＝2cm2；

    （2）若点Q从C点出发2s后点P从点A出发，再经过几秒△PCQ与△ACB相似．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

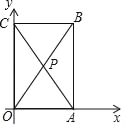
    【题目】如图，在平面直角坐标系中O是原点，矩形OABC的对角线相交于点P，顶点C的坐标是（0，3），∠ACO＝30°，将矩形OABC绕点O顺时针旋转150°后点P的对应点P′的坐标是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一空旷场地上设计一落地为矩形ABCD的小屋，AB+BC=10m，拴住小狗的10m长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S（m2）.

    （1）如图1，若BC=4m，则S=_____m2．

    （2）如图2，现考虑在（1）中矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其他条件不变，则在BC的变化过程中，当S取得最小值时，边BC的长为____m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置，点A1，A2，A3…和点C1，C2，C3…分别在直线y=x+1和x轴上，则点Bn的坐标为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商品原价为100元，第一次涨价，第二次在第一次的基础上又涨价，设平均每次增长的百分数为x，那么x应满足的方程是　　

    A. B.

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC在网格中的位置如图所示（每个小正方形边长为1），AD⊥BC于D，下列选项中，错误的是（　　）

    A. sinα＝cosα B. tanC＝2 C. sinβ＝ D. tanα＝1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

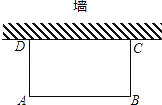
    【题目】如图，利用一面墙(墙的长度不超过45m)，用80m长的篱笆围一个矩形场地．

    (1)怎样围才能使矩形场地的面积为750m2？

    (2)能否使所围矩形场地的面积为810m2 ，为什么？

    查看答案和解析>>

    同步练习册答案