
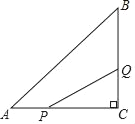
【题目】如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P从点A沿AC向C以2cm/s的速度移动,到C即停,点Q从点C沿CB向B以1cm/s的速度移动,到B就停.
(1)若P、Q同时出发,经过几秒钟S△PCQ=2cm2;
(2)若点Q从C点出发2s后点P从点A出发,再经过几秒△PCQ与△ACB相似.
【答案】(1)则P、Q同时出发,经过(2±![]() )秒钟S△PCQ=2cm2;(2)点Q从C点出发2s后点P从点A出发,再经过1.6秒或
)秒钟S△PCQ=2cm2;(2)点Q从C点出发2s后点P从点A出发,再经过1.6秒或![]() 秒秒△PCQ与△ACB相似.
秒秒△PCQ与△ACB相似.
【解析】
(1)根据题意用t表示出CQ,PC,根据三角形的面积公式列出方程,解方程即可;
(2)分△PCQ∽△ACB,△PCQ∽△BCA两种情况列出比例式,计算即可.
(1)由题意得:AP=2t,CQ=t,则PC=8﹣2t,由题意得:![]() ×(8﹣2t)×t=2,整理得:t2﹣4t+2=0,解得:t=2±
×(8﹣2t)×t=2,整理得:t2﹣4t+2=0,解得:t=2±![]() ,则P、Q同时出发,经过(2±
,则P、Q同时出发,经过(2±![]() )秒钟S△PCQ=2cm2;
)秒钟S△PCQ=2cm2;
(2)由题意得:AP=2t,CQ=2+t,则PC=8﹣2t,分两种情况讨论:
①当△PCQ∽△ACB时,![]() =
=![]() ,即
,即![]() =
=![]() ,解得:t=1.6;
,解得:t=1.6;
②当△PCQ∽△BCA时,![]() =
=![]() ,即
,即![]() =
=![]() ,解得:t=
,解得:t=![]() .
.
综上所述:点Q从C点出发2s后点P从点A出发,再经过1.6秒或![]() 秒秒△PCQ与△ACB相似.
秒秒△PCQ与△ACB相似.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:初中数学 来源: 题型:
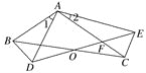
【题目】如图,△ABC≌△ADE且∠ABC=∠ADE,∠ACB=∠AED,BC、DE交于点O.则下列四个结论中,①∠1=∠2;②BC=DE;③△ABD∽△ACE;④A、O、C、E四点在同一个圆上,一定成立的有( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,m)在双曲线y=![]() 上且m<0,过点A作x轴的垂线,垂足为B.
上且m<0,过点A作x轴的垂线,垂足为B.
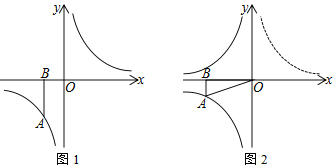
(1)如图1,当a=﹣2时,P(t,0)是x轴上的动点,将点B绕点P顺时针旋转90°至点C,
①若t=1,直接写出点C的坐标;
②若双曲线y=![]() 经过点C,求t的值.
经过点C,求t的值.
(2)如图2,将图1中的双曲线y=![]() (x>0)沿y轴折叠得到双曲线y=﹣
(x>0)沿y轴折叠得到双曲线y=﹣![]() (x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣
(x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣![]() (x<0)上的点D(d,n)处,求m和n的数量关系.
(x<0)上的点D(d,n)处,求m和n的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“富春包子”是扬州特色早点,富春茶社为了了解顾客对各种早点的喜爱情况,设计了如右图的调查问卷,对顾客进行了抽样调查.根据统计数据绘制了如下尚不完整的统计图.
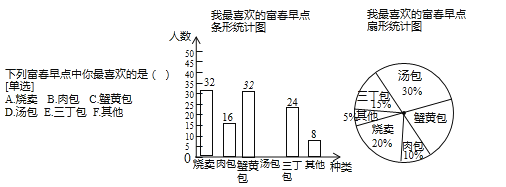
根据以上信息,解决下列问题:
(1)条形统计图中“汤包”的人数是 ,扇形统计图中“蟹黄包”部分的圆心角为 °;
(2)根据抽样调查结果,请你估计富春茶社1000名顾客中喜欢“汤包”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
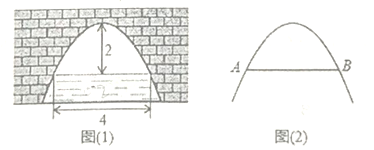
【题目】如图(1)是一个横断面为抛物线形状的拱桥,当水面宽![]() 为
为![]() 时,拱顶与水面距离为
时,拱顶与水面距离为![]() .
.
(1)请你在图(2)中,建立适当的平面直角坐标系,使该抛物线拱桥的函数关系式符合![]() 形式,并求此时,函数关系式;
形式,并求此时,函数关系式;
(2)当水面上升![]() 时,求水面宽度.
时,求水面宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3b+4c>0;④4a﹣2b≥at2+bt(t为实数);⑤点(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(﹣
,y2),(﹣![]() ,y3)是该抛物线上的点,则y1<y2<y3,其中正确的结论有( )
,y3)是该抛物线上的点,则y1<y2<y3,其中正确的结论有( )
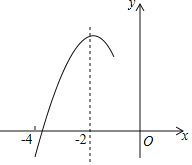
A. ②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com