
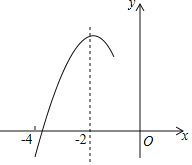
����Ŀ����ͼ��������y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x����2����x���һ�������ڣ���3��0���ͣ���4��0��֮�䣬�䲿��ͼ����ͼ��ʾ�������н��ۣ���4a��b��0����c��0���۩�3b+4c��0����4a��2b��at2+bt��tΪʵ�������ݵ㣨��![]() ��y1��������
��y1��������![]() ��y2��������
��y2��������![]() ��y3���Ǹ��������ϵĵ㣬��y1��y2��y3��������ȷ�Ľ����У�������
��y3���Ǹ��������ϵĵ㣬��y1��y2��y3��������ȷ�Ľ����У�������
A. �ڢ� B. �٢ۢܢ� C. �٢ڢۢ� D. �٢ڢۢ�
���𰸡�D
��������
���������ߵĶԳ�����жϢ٣�����������x��Ľ��㼰�����ߵĶԳ��Կ��жϢڣ���x����1ʱy��0���жϢۣ���x����2ʱ����ȡ�����ֵ���жϢܣ����������ߵĿ��������ҶԳ���Ϊֱ��x����2֪ͼ������Գ���ˮƽ����ԽС����ֵԽ���жϢݣ�
�������ߵĶԳ���Ϊֱ��x����![]() ����2��
����2��
��4a��b��0�����Ԣ���ȷ��
����x���һ�������ڣ���3��0���ͣ���4��0��֮�䣬
���������ߵĶԳ���֪����һ�������ڣ���1��0���ͣ�0��0��֮�䣬
����������y��Ľ�����y��ĸ����ᣬ��c��0���ʢ���ȷ��
���ɢ�֪��x����1ʱy��0����b��4a��
��a��b+c��![]() b��b+c����
b��b+c����![]() b+c��0��
b+c��0��
����3b+4c��0��
���Ԣ���ȷ��
�ɺ���ͼ��֪��x����2ʱ������ȡ�����ֵ��
��4a��2b+c��at2+bt+c��
��4a��2b��at2+bt��tΪʵ�������ʢ���ȷ��
�������ߵĿ������£��ҶԳ���Ϊֱ��x����2��
������������Գ���ˮƽ����ԽС������ֵԽ��
��y1��y3��y2���ʢݴ���
��ѡ��D��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
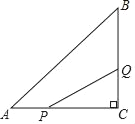
����Ŀ����ͼ������ABC�У���C��90����AC��8cm��BC��6cm����P�ӵ�A��AC��C��2cm/s���ٶ��ƶ�����C��ͣ����Q�ӵ�C��CB��B��1cm/s���ٶ��ƶ�����B��ͣ��
��1����P��Qͬʱ����������������S��PCQ��2cm2��
��2������Q��C�����2s���P�ӵ�A�������پ���������PCQ����ACB���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒԭ��Ϊ100Ԫ����һ���Ǽ�![]() ���ڶ����ڵ�һ�εĻ��������Ǽ�
���ڶ����ڵ�һ�εĻ��������Ǽ�![]() ����ƽ��ÿ�������İٷ���Ϊx����ôxӦ����ķ�����
����ƽ��ÿ�������İٷ���Ϊx����ôxӦ����ķ�����![]() ����
����![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�������е�λ����ͼ��ʾ��ÿ��С�����α߳�Ϊ1����AD��BC��D������ѡ���У�������ǣ�������

A. sin����cos�� B. tanC��2 C. sin����![]() D. tan����1
D. tan����1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y��![]() x��2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y��
x��2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y��![]() x2+bx+c����A��C���㣬��x�����һ����Ϊ��B��
x2+bx+c����A��C���㣬��x�����һ����Ϊ��B��
��1���������ߵĺ�������ʽ��
��2����DΪֱ��AC�·���������һ�㣬�ҡ�ACD��2��BAC�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
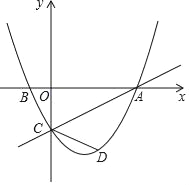
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y��![]() x��2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y��
x��2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y��![]() x2+bx+c����A��C���㣬��x�����һ����Ϊ��B��
x2+bx+c����A��C���㣬��x�����һ����Ϊ��B��
��1���������ߵĺ�������ʽ��
��2����DΪֱ��AC�·���������һ�㣬�ҡ�ACD��2��BAC�����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��������ABC�У���ACB=900��AB=10�� BC=6�����߶�AB��ȡһ��D����DF��AB��AC�ڵ�F.�ֽ���ADF��DF�۵���ʹ��A�����߶�DB�ϣ���Ӧ���ΪA1��AD���е�E�Ķ�Ӧ���ΪE1.����E1FA1�ס�E1BF����AD= .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
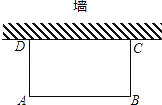
����Ŀ����ͼ������һ��ǽ(ǽ�ij��Ȳ�����45m)����80m�������Χһ�����γ��أ�
(1)����Χ����ʹ���γ��ص����Ϊ750m2��
(2)�ܷ�ʹ��Χ���γ��ص����Ϊ810m2 ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������и��⣺
(1)������ֱ�����ľ�˼ס��ҡ�������·�����ҡ�����Ӱ����ͼ1��ʾ����ȷ��·�Ƶ��ݵ�λ�ã���������Ӱ�ӣ�(��д������������ͼ�ۼ�)

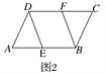
(2)��ͼ2����ƽ���ı���ABCD�У���E��F�ֱ���AB��CD�ϣ�AE��CF.��֤��DE��BF.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com