
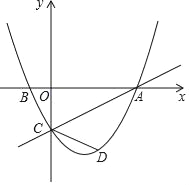
【题目】如图,在平面直角坐标系中,直线y=![]() x﹣2与x轴交于点A,与y轴交于点C,抛物线y=
x﹣2与x轴交于点A,与y轴交于点C,抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC下方抛物线上一点,且∠ACD=2∠BAC,求点D的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)D(2,﹣3)
x﹣2;(2)D(2,﹣3)
【解析】
(1)求出A、C两点坐标,利用待定系数法即可解决问题;
(2)过点D作DF∥x轴,交y轴于点E,则∠CFD=∠BAC,推出∠CDF=∠CFD,可得∠ACD=2∠BAC,由此利用三角函数构建方程即可解决问题;
解:(1)直线y=![]() x﹣2与x轴交于点A, 与y轴交于点C,x=0时,y=-2,y=0时,x=4,所以A(4,0),C(0,﹣2),
x﹣2与x轴交于点A, 与y轴交于点C,x=0时,y=-2,y=0时,x=4,所以A(4,0),C(0,﹣2),
把A(4,0),C(0,-2)代入y=![]() x2+bx+c,得到
x2+bx+c,得到![]() ,
,
解得 ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣2.
x﹣2.
(2)过点D作DF∥x轴,交y轴于点E,则∠CFD=∠BAC,
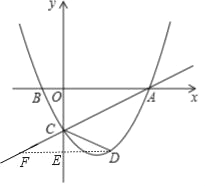
∵∠ACD=2∠BAC=∠CFD+∠CDF,
∴∠CDF=∠CFD,
∴tan∠CDF=tan∠BAC=![]() ,
,
∴![]()
解得x=2,
∴D(2,﹣3).


科目:初中数学 来源: 题型:
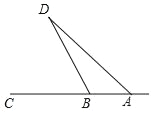
【题目】美丽的甬江宛如一条玉带穿城而过,数学课外实践活动中,小林在甬江岸边的A, B两点处,利用测角仪分别对西岸的一观景亭D进行测量.如图,测得∠DAC=45°,∠DBC=65°,若AB=114米,求观景亭D到甬江岸边AC的距离约为多少米?
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3b+4c>0;④4a﹣2b≥at2+bt(t为实数);⑤点(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(﹣
,y2),(﹣![]() ,y3)是该抛物线上的点,则y1<y2<y3,其中正确的结论有( )
,y3)是该抛物线上的点,则y1<y2<y3,其中正确的结论有( )
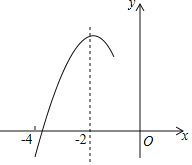
A. ②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点D是BC的中点
,点D是BC的中点![]() 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
![]() 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______;
![]() 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转![]() ,
,
![]() 判断
判断![]() 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论;
![]() 若
若![]() ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD平分∠BAC,AB=AC,连接BC,交AD于点E,下列说法正确的有( )
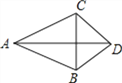
①∠BAC=∠ACB;②S四边形ABDC=ADCE;③AB2+CD2=AC2+BD2;④AB﹣BD=AC﹣CD.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社推出一条成本价为500元/人的省内旅游线路.游客人数![]() (人/月)与旅游报价
(人/月)与旅游报价![]() (元/人)之间的关系为
(元/人)之间的关系为![]() ,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com