
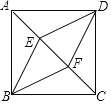
【题目】如图,E、F是正方形ABCD对角线AC上的两点,且![]() ,连接BE、DE、BF、DF.
,连接BE、DE、BF、DF.
![]() 求证:四边形BEDF是菱形:
求证:四边形BEDF是菱形:
![]() 求
求![]() 的值.
的值.
【答案】(1)证明见解析(2)3
【解析】
(1)连接BD交AC于点O,根据正方形的性质得到OA=OC,OB=OD,AC⊥BD,证明OE=OF,得到四边形BEDF是平行四边形,根据菱形的判定定理证明;
(2)根据正方形的性质得到OD=3OF,根据正切的定义计算,得到答案.
(1)连接BD交AC于点O.
∵四边形ABCD是正方形,∴OA=OC,OB=OD,且AC⊥BD.
∵AE=CF,∴OA﹣AE=OC﹣CF,即OE=OF.
又∵OB=OD,∴四边形BEDF是平行四边形.
又∵AC⊥BD,∴平行四边形BEDF是菱形;
(2)∵EF=2OF,EF=CF,∴CF=2OF,∴OC=3OF.
又∵OD=OC,∴OD=3OF.
在正方形ABCD中,AC⊥BD,∴∠DOF=90°.在Rt△DOF中,tan∠AFD![]() 3.
3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
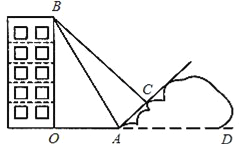
【题目】某校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动.如图,她在山坡坡脚A出测得这座楼房的楼顶B点的仰角为60°,沿山坡往上走到C处再测得B点的仰角为45°.已知OA=200m,此山坡的坡比i=![]() ,且O、A、D在同一条直线上.
,且O、A、D在同一条直线上.
求:(1)楼房OB的高度;
(2)小红在山坡上走过的距离AC.(计算过程和结果均不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
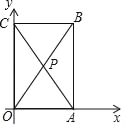
【题目】如图,在平面直角坐标系中O是原点,矩形OABC的对角线相交于点P,顶点C的坐标是(0,3),∠ACO=30°,将矩形OABC绕点O顺时针旋转150°后点P的对应点P′的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
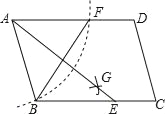
【题目】如图,四边形ABCD是平行四边形,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则∠AEB的正切值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )

A. sinα=cosα B. tanC=2 C. sinβ=![]() D. tanα=1
D. tanα=1
查看答案和解析>>
科目:初中数学 来源: 题型:
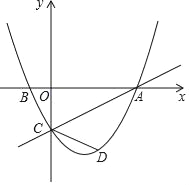
【题目】如图,在平面直角坐标系中,直线y=![]() x﹣2与x轴交于点A,与y轴交于点C,抛物线y=
x﹣2与x轴交于点A,与y轴交于点C,抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC下方抛物线上一点,且∠ACD=2∠BAC,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com