
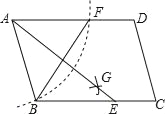
【题目】如图,四边形ABCD是平行四边形,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则∠AEB的正切值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
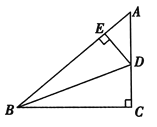
【题目】如图,在△ABC中,∠C=90°,点D,E分别在AC,AB上,BD平分∠ABC,DE⊥AB于点E,AE=6,cosA=![]() .
.
(1)求CD的长;
(2)求tan∠DBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=![]() ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60,AB=30。点D是AC上的动点,过D作DF⊥BC于F,再过F作FE//AC,交AB于E。设CD=x,DF=y.
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当△FED是直角三角形时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣mx﹣(m+1)与x轴负半轴交于点A(x1,0),与x轴正半轴交于点B(x2,0)(OA<OB),与y轴交于点C,且满足x12+x22﹣x1x2=13.
(1)求抛物线的解析式;
(2)以点B为直角顶点,BC为直角边作Rt△BCD,CD交抛物线于第四象限的点E,若EC=ED,求点E的坐标;
(3)在抛物线上是否存在点Q,使得S△ACQ=2S△AOC?若存在,求出点Q的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
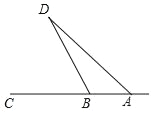
【题目】美丽的甬江宛如一条玉带穿城而过,数学课外实践活动中,小林在甬江岸边的A, B两点处,利用测角仪分别对西岸的一观景亭D进行测量.如图,测得∠DAC=45°,∠DBC=65°,若AB=114米,求观景亭D到甬江岸边AC的距离约为多少米?
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点D是BC的中点
,点D是BC的中点![]() 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
![]() 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______;
![]() 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转![]() ,
,
![]() 判断
判断![]() 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论;
![]() 若
若![]() ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com