
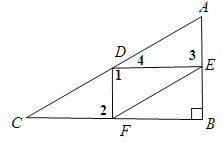
【题目】如图,在Rt△ABC中,∠B=90°,AC=60,AB=30。点D是AC上的动点,过D作DF⊥BC于F,再过F作FE//AC,交AB于E。设CD=x,DF=y.
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当△FED是直角三角形时,求x的值.

【答案】(1)![]() ;(2)40;(3)30.
;(2)40;(3)30.
【解析】
试题(1)由已知,根据锐角三角函数定义和特殊角的三角函数值可得∠C=30°,从而在Rt△CDF中,再应用锐角三角函数定义和特殊角的三角函数值可得y与x的函数关系式.
(2)根据菱形四边相等的性质,由AD=DF即AC-CD=DF列方程求解.
(3)首先判断△FED是直角三角形只有∠FDE=90°,得出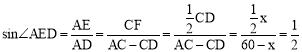 ,解之即为所求.
,解之即为所求.
试题解析:(1)∵∠B=90°,AC=60,AB=30,
∴![]() .∴∠C=30°.∴
.∴∠C=30°.∴![]() .
.
∴y与x的函数关系式为![]() .
.
(2)当四边形AEFD为菱形时,有AD=DF,
∴AC-CD=DF,即![]() ,解得x=40.
,解得x=40.
∴当四边形AEFD为菱形时,x=40.
(3)如图,当△FED直角三角形是时,只能是∠FDE=90°,
∵DF⊥BC,∠B=90°,∴DF//AB.
又∵FE//AC,∴四边形AEFD为平行四边形. ∴AE=DF.
由DF⊥BC得∠2=90°,∴∠1=∠2. ∴DE//BC.
∴∠3=∠B=90°,∠4=∠C=30°.
在Rt△BOC中,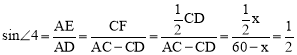 ,即60-x= x,
,即60-x= x,
∴x=30.
∴当△FED是直角三角形时,x=30.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形,
的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形, ![]() 是一个格点三角形.
是一个格点三角形.
![]() 在图
在图![]() 中,请判断
中,请判断![]() 与
与![]() 是否相似,并说明理由;
是否相似,并说明理由;
![]() 在图
在图![]() 中,以O为位似中心,再画一个格点三角形,使它与
中,以O为位似中心,再画一个格点三角形,使它与![]() 的位似比为2:1
的位似比为2:1
![]() 在图
在图![]() 中,请画出所有满足条件的格点三角形,它与
中,请画出所有满足条件的格点三角形,它与![]() 相似,且有一条公共边和一个公共角.
相似,且有一条公共边和一个公共角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
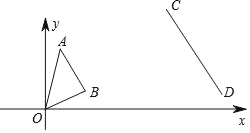
A. (0,0) B. (3,4)或(﹣6,2)
C. (5,3)或(-7,1) D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=﹣x2+mx+n,直线y2=kx+b,y1的对称轴与y2交于点A(﹣1,5),点A与y1的顶点B的距离是4.
(1)求y1的解析式;
(2)若y2随着x的增大而增大,且y1与y2都经过x轴上的同一点,求y2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
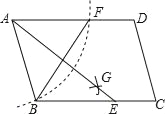
【题目】如图,四边形ABCD是平行四边形,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则∠AEB的正切值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )
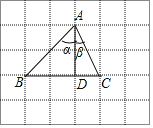
A. sinα=cosα B. tanC=2 C. sinβ=![]() D. tanα=1
D. tanα=1
查看答案和解析>>
科目:初中数学 来源: 题型:
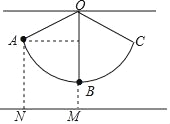
【题目】如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
【答案】15cm
【解析】
试题设细线OB的长度为xcm,作AD⊥OB于D,证出四边形ANMD是矩形,得出AN=DM=14cm,求出OD=x-9,在Rt△AOD中,由三角函数得出方程,解方程即可.
试题解析:设细线OB的长度为xcm,作AD⊥OB于D,如图所示:
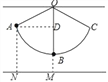
∴∠ADM=90°,
∵∠ANM=∠DMN=90°,
∴四边形ANMD是矩形,
∴AN=DM=14cm,
∴DB=14﹣5=9cm,
∴OD=x﹣9,
在Rt△AOD中,cos∠AOD=![]() ,
,
∴cos66°=![]() =0.40,
=0.40,
解得:x=15,
∴OB=15cm.
【题型】解答题
【结束】
20
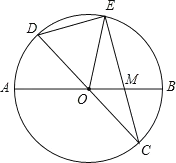
【题目】已知:如图,在半径为![]() 的
的![]() 中,
中,![]() 、
、![]() 是两条直径,
是两条直径,![]() 为
为![]() 的中点,
的中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() 。
。![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com