
【题目】二次函数![]() 的图象如图所示,下列结论:
的图象如图所示,下列结论:![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ,其中正确结论的是
,其中正确结论的是![]()
![]()
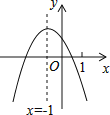
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AD平分∠BAC,AB=AC,连接BC,交AD于点E,下列说法正确的有( )
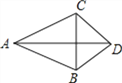
①∠BAC=∠ACB;②S四边形ABDC=ADCE;③AB2+CD2=AC2+BD2;④AB﹣BD=AC﹣CD.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社推出一条成本价为500元/人的省内旅游线路.游客人数![]() (人/月)与旅游报价
(人/月)与旅游报价![]() (元/人)之间的关系为
(元/人)之间的关系为![]() ,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
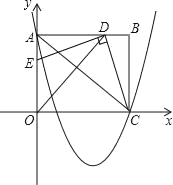
【题目】如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,C在x轴的正半轴上,已知A(0,8)、C(10,0),作∠AOC的平分线交AB于点D,连接CD,过点D作DE⊥CD交OA于点E.
(1)求点D的坐标;
(2)求证:△ADE≌△BCD;
(3)抛物线y=![]() x2﹣
x2﹣![]() x+8经过点A、C,连接AC.探索:若点P是x轴下方抛物线上一动点,过点P作平行于y轴的直线交AC于点M.是否存在点P,使线段MP的长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
x+8经过点A、C,连接AC.探索:若点P是x轴下方抛物线上一动点,过点P作平行于y轴的直线交AC于点M.是否存在点P,使线段MP的长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
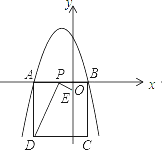
【题目】二次函数y=![]() 的图象与x轴交于点A和点B,以AB为边在x轴下方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A和点B,以AB为边在x轴下方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)求出m的值并求出点A、点B的坐标.
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com