
【题目】要使关于x的方程![]() 有两个实数根,且使关于x的分式方程
有两个实数根,且使关于x的分式方程![]() 的解为非负数的所有整数a的个数为
的解为非负数的所有整数a的个数为![]()
![]()
A. 3个B. 4个C. 5个D. 6个
【答案】B
【解析】
根据判别式的意义得到a≠0且△=(-2)2-4a(-1)≥0,解得a≥-1且a≠0,再把分式方程化为x-(a+2)=2(x-3),解得x=-a+4,利用分式方程的解为非负数得到-a+4≥0且-a+4≠3,解得a≤4且a≠1,所以-1≤a≤4且a≠0,然后写出此范围内的整数即可.
解:∵关于x的方程ax2-2x-1=0有两个实数根,
∴a≠0且△=(-2)2-4a(-1)≥0,
∴a≥-1且a≠0,
对于分式方程![]() ,
,
去分母得x-(a+2)=2(x-3),
解得x=-a+4,
因为分式方程的解为非负数,
所以-a+4≥0且-a+4≠3,解得a≤4且a≠1,
所以-1≤a≤4且a≠0,
所以整数a的值为-1,2,3,4.
故选:B.


科目:初中数学 来源: 题型:
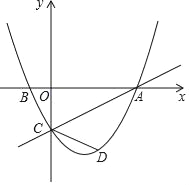
【题目】如图,在平面直角坐标系中,直线y=![]() x﹣2与x轴交于点A,与y轴交于点C,抛物线y=
x﹣2与x轴交于点A,与y轴交于点C,抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC下方抛物线上一点,且∠ACD=2∠BAC,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
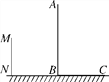
【题目】操场上有三根测杆AB,MN和XY,MN=XY,其中测杆AB在太阳光下某一时刻的影子为BC(如图中粗线).
(1)画出测杆MN在同一时刻的影子NP(用粗线表示),并简述画法;
(2)若在同一时刻测杆XY的影子的顶端恰好落在点B处,画出测杆XY所在的位置(用实线表示),并简述画法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列各题:
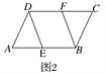
(1)三根垂直地面的木杆甲、乙、丙,在路灯下乙、丙的影子如图1所示.试确定路灯灯泡的位置,再作出甲的影子.(不写作法,保留作图痕迹)

(2)如图2,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个整数,将其末三位截去,这个末三位数与余下的数的7倍的差能被19整除,则这个数能被19整除,否则不能被19整除,能被19整除的我们称之为“灵异数”.
如46379,由![]() ,
,![]() 能被19整除,
能被19整除,![]() 能被19整除,是“灵异数”.
能被19整除,是“灵异数”.
![]() 请用上述规则判断52478和9115是否为“灵异数”;
请用上述规则判断52478和9115是否为“灵异数”;
![]() 有一个首位数字是1的五位正整数,它的个位数字不为0且是千位数字的2倍,十位和百位上的数字之和为8,若这个数恰好是“灵异数”,请求出这个数.
有一个首位数字是1的五位正整数,它的个位数字不为0且是千位数字的2倍,十位和百位上的数字之和为8,若这个数恰好是“灵异数”,请求出这个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题.
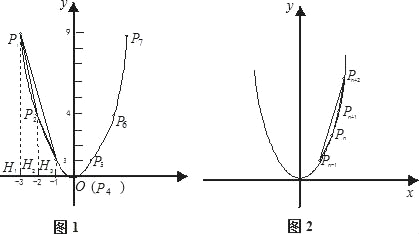
材料:“小聪设计的一个电子游戏是:一电子跳蚤从这P1(﹣3,9)开始,按点的横坐标依次增加1的规律,在抛物线y=x2上向右跳动,得到点P2、P3、P4、P5…(如图1所示).过P1、P2、P3分别作P1H1、P2H2、P3H3垂直于x轴,垂足为H1、H2、H3,则S△P1P2P3=S梯形P1H1H3P3﹣S梯形P1H1H2P2﹣S梯形P2H2H3P3=![]() (9+1)×2﹣
(9+1)×2﹣![]() (9+4)×1﹣
(9+4)×1﹣![]() (4+1)×1,即△P1P2P3的面积为1.”
(4+1)×1,即△P1P2P3的面积为1.”
问题:
(1)求四边形P1P2P3P4和P2P3P4P5的面积(要求:写出其中一个四边形面积的求解过程,另一个直接写出答案);
(2)猜想四边形Pn﹣1PnPn+1Pn+2的面积,并说明理由(利用图2);
(3)若将抛物线y=x2改为抛物线y=x2+bx+c,其它条件不变,猜想四边形Pn﹣1PnPn+1Pn+2的面积(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
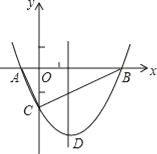
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com