
【题目】如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,C在x轴的正半轴上,已知A(0,8)、C(10,0),作∠AOC的平分线交AB于点D,连接CD,过点D作DE⊥CD交OA于点E.
(1)求点D的坐标;
(2)求证:△ADE≌△BCD;
(3)抛物线y=![]() x2﹣
x2﹣![]() x+8经过点A、C,连接AC.探索:若点P是x轴下方抛物线上一动点,过点P作平行于y轴的直线交AC于点M.是否存在点P,使线段MP的长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
x+8经过点A、C,连接AC.探索:若点P是x轴下方抛物线上一动点,过点P作平行于y轴的直线交AC于点M.是否存在点P,使线段MP的长度有最大值?若存在,求出点P的坐标;若不存在,请说明理由.
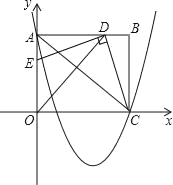
【答案】(1)(8,8);(2)详见解析;(3)存在,P点坐标为(5,﹣6).
【解析】
(1)利用角平分线的性质以及矩形的性质得出∠ADO=∠DOC,以及∠AOD=∠ADO,进而得出答案;
(2)利用全等三角形的判定方法(ASA)即可得出答案;
(3)设P点坐标为(t,![]() t2﹣
t2﹣![]() t+8),设AC所在的直线的函数关系式为y=kx+b,根据A(0,8)、C(10,0),求出AC的解析式,进而用t表示出PM的长,利用二次函数的性质求出PM的最值,点P的坐标也可以求出.
t+8),设AC所在的直线的函数关系式为y=kx+b,根据A(0,8)、C(10,0),求出AC的解析式,进而用t表示出PM的长,利用二次函数的性质求出PM的最值,点P的坐标也可以求出.
解:(1)∵OD平分∠AOC,∴∠AOD=∠DOC.
∵四边形AOCB是矩形,
∴AB∥OC
∴∠AOD=∠DOC
∴∠AOD=∠ADO.
∴OA=AD(等角对等边).
∵A点的坐标为(0,8),
∴D点的坐标为(8,8)
(2)∵四边形AOCB是矩形,
∴∠OAB=∠B=90°,BC=OA.
∵OA=AD,
∴AD=BC.
∵ED⊥DC
∴∠EDC=90°
∴∠ADE+∠BDC=90°
∴∠BDC+∠BCD=90°.
∴∠ADE=∠BCD.
在△ADE和△BCD中,
∵∠DAE=∠B,AD=BC,∠ADE=∠BCD,
∴△ADE≌△BCD(ASA)
(3)存在,
∵二次函数的解析式为:,点P是抛物线上的一动点,
∴设P点坐标为(t,![]() t2﹣
t2﹣![]() t+8)
t+8)
设AC所在的直线的函数关系式为y=kx+b,
∵A(0,8)、C(10,0),
∴![]() ,解得
,解得
∴直线AC的解析式y=-![]() .
.
∵PM∥y轴,
∴M(t,-![]() ).
).
∴PM=﹣( ![]() t2﹣
t2﹣![]() t+8)+(-
t+8)+(-![]() )=-
)=-![]() (t-5)2+10.
(t-5)2+10.
∴当t=5时,PM有最大值为10.
∴所求的P点坐标为(5,﹣6).


科目:初中数学 来源: 题型:
【题目】△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )

A. sinα=cosα B. tanC=2 C. sinβ=![]() D. tanα=1
D. tanα=1
查看答案和解析>>
科目:初中数学 来源: 题型:
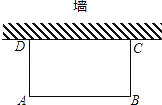
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
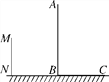
【题目】操场上有三根测杆AB,MN和XY,MN=XY,其中测杆AB在太阳光下某一时刻的影子为BC(如图中粗线).
(1)画出测杆MN在同一时刻的影子NP(用粗线表示),并简述画法;
(2)若在同一时刻测杆XY的影子的顶端恰好落在点B处,画出测杆XY所在的位置(用实线表示),并简述画法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列各题:
(1)三根垂直地面的木杆甲、乙、丙,在路灯下乙、丙的影子如图1所示.试确定路灯灯泡的位置,再作出甲的影子.(不写作法,保留作图痕迹)

(2)如图2,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题.
材料:“小聪设计的一个电子游戏是:一电子跳蚤从这P1(﹣3,9)开始,按点的横坐标依次增加1的规律,在抛物线y=x2上向右跳动,得到点P2、P3、P4、P5…(如图1所示).过P1、P2、P3分别作P1H1、P2H2、P3H3垂直于x轴,垂足为H1、H2、H3,则S△P1P2P3=S梯形P1H1H3P3﹣S梯形P1H1H2P2﹣S梯形P2H2H3P3=![]() (9+1)×2﹣
(9+1)×2﹣![]() (9+4)×1﹣
(9+4)×1﹣![]() (4+1)×1,即△P1P2P3的面积为1.”
(4+1)×1,即△P1P2P3的面积为1.”
问题:
(1)求四边形P1P2P3P4和P2P3P4P5的面积(要求:写出其中一个四边形面积的求解过程,另一个直接写出答案);
(2)猜想四边形Pn﹣1PnPn+1Pn+2的面积,并说明理由(利用图2);
(3)若将抛物线y=x2改为抛物线y=x2+bx+c,其它条件不变,猜想四边形Pn﹣1PnPn+1Pn+2的面积(直接写出答案).
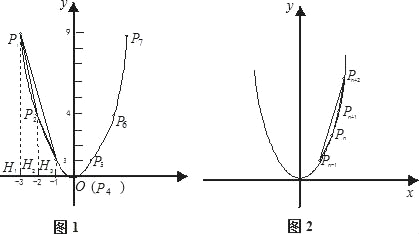
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼![]() (可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点
(可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点![]() 和点
和点![]() 处,
处,![]() 、
、![]() 均在
均在![]() 的中垂线上,且
的中垂线上,且![]() 、
、![]() 到大楼的距离分别为
到大楼的距离分别为![]() 米和
米和![]() 米,又已知
米,又已知![]() 长
长![]() 米,
米,![]() 长
长![]() 米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.
米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com